【题目】如图,直线l与⊙O交于C,D两点,且与半径OA垂直,垂足为H,∠ODC=30°,在OD的延长线上取一点B,使得AD=BD,若⊙O的半径为2,则图中阴影部分的面积为(结果保留π) 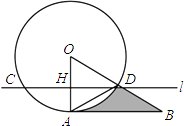
参考答案:
【答案】2 ![]() ﹣
﹣ ![]() π
π
【解析】解:直线AB与⊙O的位置关系是相切, 理由是:∵AO⊥CD,
∴∠OAD=90°,
∵∠ODC=30°,
∴∠DOA=60°,
∵OA=OD,
∴△OAD是等边三角形,
∴∠OAD=∠ODA=60°,
∵AD=BD,
∴∠DAB=∠B,
∵∠ODA=∠B+∠DAB,
∴∠DAB=∠B=30°,
∴∠OAB=30°+60°=90°,
∵∠B=30°,∠OAB=90°,OA=2,
∴OB=2OA=4,由勾股定理得:AB=2 ![]() ,
,
∴阴影部分的面积S=S△OAB﹣S扇形OAD= ![]() ×2
×2 ![]() ×2﹣
×2﹣ ![]() =2
=2 ![]() ﹣
﹣ ![]() π.
π.
所以答案是:2 ![]() ﹣
﹣ ![]() π.
π.
【考点精析】掌握扇形面积计算公式是解答本题的根本,需要知道在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一个八角星形纸板,图中有八个直角、八个相等的钝角,每条边都相等,如图2将纸板沿虚线进行切割,无缝隙无重叠的拼成如图3所示的大正方形,其面积为8+4
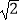 ,则图3中线段AB的长为( )
,则图3中线段AB的长为( ) 
A.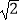
B.2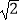
C.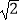 ﹣1
﹣1
D.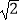 +1
+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算(1)
 (2)
(2)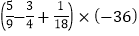
(3) 9+(—7)+10+(—3)+(—9) (4)


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某年6月份的日历.
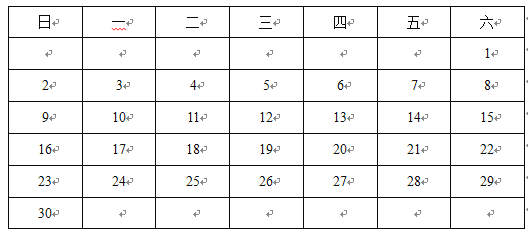
(1)细心观察:小张一家外出旅游5天,这5天的日期之和是20.小张旅游最后一天是 _____________号.
(2)如果用一个长方形方框任意框出3
 3个数,从左下角到右上角的“对角线”上的3个数字的和54,那么这9个数的和为______________,在这9个日期中,最后一天是_____________号.
3个数,从左下角到右上角的“对角线”上的3个数字的和54,那么这9个数的和为______________,在这9个日期中,最后一天是_____________号.
(3)在这个月的日历中,用方框能否圈出“总和为135”的9个数?如果能,请求出这9个日期分别是几号;如果不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,∠BAD的平分线交直线BC于点E,交直线DC的延长线于点F,以EC、CF为邻边作□ECFG.
(1)如图1,证明□ECFG为菱形;
(2)如图2,若∠ABC=120°,连接BG、CG,求证△DGC≌△BGE,并求出∠BDG的度数;
(3)如图3,若∠ABC=90°,M是EF的中点,请直接写出∠BDM的度数.
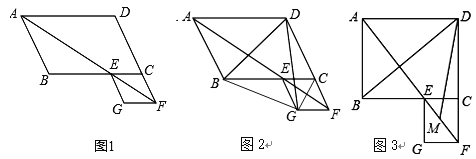
-
科目: 来源: 题型:
查看答案和解析>>【题目】适合下列条件的△ABC中,直角三角形的个数为( )
①a=
 ,b=
,b= ,c=
,c= ; ②a=b,∠A=45°; ③a=2,b=2,c=
; ②a=b,∠A=45°; ③a=2,b=2,c= ;④∠A=27°,∠B=63°;⑤a=9,b=12,c=15
;④∠A=27°,∠B=63°;⑤a=9,b=12,c=15A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,BC=12,CD=9,将△ABE沿BE折叠,使点A恰好落在对角线BD上的F处,则DE的长是( )

A.
 B.
B.  C.
C.  D.
D. 
相关试题

