【题目】如图,矩形ABCD中,BC=12,CD=9,将△ABE沿BE折叠,使点A恰好落在对角线BD上的F处,则DE的长是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】C
【解析】分析:由ABCD为矩形,得到∠BAD为直角,且三角形BEF与三角形BAE全等,利用全等三角形对应角、对应边相等得到EF⊥BD,AE=EF,AB=BF,利用勾股定理求出BD的长,由BD-BF求出DF的长,在Rt△EDF中,设EF=x,表示出ED,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即可确定出DE的长.
详解:∵矩形ABCD,
∴∠BAD=90°,
由折叠可得△BEF≌△BAE,
∴EF⊥BD,AE=EF,AB=BF,
在Rt△ABD中,AB=CD=9,BC=AD=12,
根据勾股定理得:BD=15,即FD=15-9=6,
设EF=AE=x,则有ED=12-x,
根据勾股定理得:x2+62=(12-x)2,
解得:x=![]() ,
,
则DE=12-![]() =
=![]() ,
,
故选C.
-
科目: 来源: 题型:
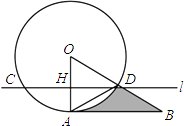
查看答案和解析>>【题目】如图,直线l与⊙O交于C,D两点,且与半径OA垂直,垂足为H,∠ODC=30°,在OD的延长线上取一点B,使得AD=BD,若⊙O的半径为2,则图中阴影部分的面积为(结果保留π)
-
科目: 来源: 题型:
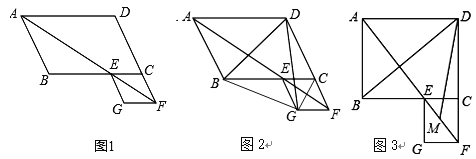
查看答案和解析>>【题目】在□ABCD中,∠BAD的平分线交直线BC于点E,交直线DC的延长线于点F,以EC、CF为邻边作□ECFG.
(1)如图1,证明□ECFG为菱形;
(2)如图2,若∠ABC=120°,连接BG、CG,求证△DGC≌△BGE,并求出∠BDG的度数;
(3)如图3,若∠ABC=90°,M是EF的中点,请直接写出∠BDM的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】适合下列条件的△ABC中,直角三角形的个数为( )
①a=
 ,b=
,b= ,c=
,c= ; ②a=b,∠A=45°; ③a=2,b=2,c=
; ②a=b,∠A=45°; ③a=2,b=2,c= ;④∠A=27°,∠B=63°;⑤a=9,b=12,c=15
;④∠A=27°,∠B=63°;⑤a=9,b=12,c=15A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘海上巡逻船在A地巡航,这时接到B地海上指挥中心紧急通知:在指挥中心北偏西60°方向的C地有一艘渔船遇险,要求马上前去救援,要求马上前去救援.此时C地位于A地北偏西30°方向上,A地位于B地北偏西75°方向上,A、B两地之间的距离为12海里,则A、C两地之间的距离为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线AB与x轴交于点A,与y轴交于点B,点A的坐标为(3,0),点B的坐标为(0,4),点P为双曲线y=
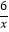 (x>0)上的一点,过点P分别作x轴、y轴的垂线段PE、PF,当PE、PF分别与线段AB交于点C、D时,ADBC的值为
(x>0)上的一点,过点P分别作x轴、y轴的垂线段PE、PF,当PE、PF分别与线段AB交于点C、D时,ADBC的值为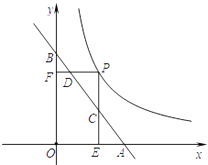
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在纸面上有一数轴(如图),折叠纸面.
(1)若1表示的点与-1表示的点重合,则-2表示的点与数 表示的点重合;
(2)若-1表示的点与5表示的点重合,回答以下问题:
① 7表示的点与数 表示的点重合;
② 若数轴上A、B两点之间的距离为11(A在B的左侧),且A、B两点经折叠后
重合, 求A、B两点表示的数各是多少?

相关试题

