【题目】(探索新知)
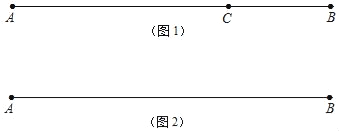
如图1,点C在线段AB上,图中共有3条线段:AB、AC和BC,若其中有一条线段的长度是另一条线段长度的两倍,则称点C是线段AB的“二倍点”.
(1)一条线段的中点 这条线段的“二倍点”;(填“是”或“不是”)
(深入研究)
如图2,若线段AB=20cm,点M从点B的位置开始,以每秒2cm的速度向点A运动,当点M到达点A时停止运动,运动的时间为t秒.
(2)问t为何值时,点M是线段AB的“二倍点”;
(3)同时点N从点A的位置开始,以每秒1cm的速度向点B运动,并与点M同时停止.请直接写出点M是线段AN的“二倍点”时t的值.
参考答案:
【答案】(1)是;(2)t为![]() 或5或
或5或![]() 时;(3)t为7.5或8或
时;(3)t为7.5或8或![]() 时
时
【解析】
(1)可直接根据“二倍点”的定义进行判断即可;
(2)用含t的代数式分别表示出线段AM、BM、AB,然后根据“二倍点”的意义,分类讨论即可得结果;
(3)用含t的代数式分别表示出线段AN、NM、AM,然后根据“二倍点”的意义,分类讨论即可.
(1)因为线段的中点把该线段分成相等的两部分,
该线段等于2倍的中点一侧的线段长,
所以一条线段的中点是这条线段的“二倍点”,
故答案为:是;
(2)当AM=2BM时,20﹣2t=2×2t,解得:t=![]() ;
;
当AB=2AM时,20=2×(20﹣2t),解得:t=5;
当BM=2AM时,2t=2×(20﹣2t),解得:t=![]() ;
;
答:t为![]() 或5或
或5或![]() 时,点M是线段AB的“二倍点”;
时,点M是线段AB的“二倍点”;
(3)当AN=2MN时,t=2[t﹣(20﹣2t)],解得:t=8;
当AM=2NM时,20﹣2t=2[t﹣(20﹣2t)],解得:t=7.5;
当MN=2AM时,t﹣(20﹣2t)=2(20﹣2t),解得:t=![]() ;
;
答:t为7.5或8或![]() 时,点M是线段AN的“二倍点”.
时,点M是线段AN的“二倍点”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段CD在线段AB上,且CD=2,若线段AB的长度是一个正整数,则图中以A,B,C,D这四点中任意两点为端点的所有线段长度之和可能是( )

A. 29
B. 28
C. 30
D. 31
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①若
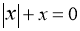 则
则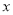 为负数;②若关于的方程
为负数;②若关于的方程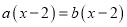 有无数解,则a=b;③若
有无数解,则a=b;③若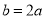 ,则关于
,则关于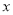 的方程
的方程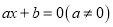 的解为
的解为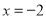 ;④若
;④若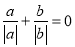 则
则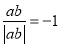 ;⑥若
;⑥若 ,且
,且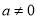 ,则
,则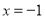 一定是为程
一定是为程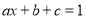 的解;其中结论正确个数有( )
的解;其中结论正确个数有( )A.4个B.3个C.2个D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高学生书写汉字的能力,增强保护汉子的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为
 (分),且
(分),且 ,将其按分数段分为五组,绘制出以下不完整表格:
,将其按分数段分为五组,绘制出以下不完整表格:组别
成绩
 (分)
(分)频数(人数)
频率
一

2
0.04
二

10
0.2
三
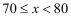
14
b
四

a
0.32
五

8
0.16
请根据表格提供的信息,解答以下问题: (1)本次决赛共有 名学生参加;
(2)直接写出表中a= ,b= ;
(3)请补全下面相应的频数分布直方图;

(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为 。
-
科目: 来源: 题型:
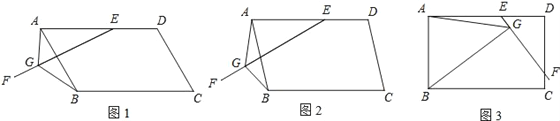
查看答案和解析>>【题目】在ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
(1)如图1,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;
(2)如图2,当EF与AB相交时,若∠EAB=α(0°<α<90°),请你直接写出线段EG、AG、BG之间的数量关系(用含α的式子表示);
(3)如图3,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,E,F是对角线BD上的两点,如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )
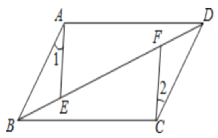
A. AE=CFB. BE=FDC. BF=DED. ∠1=∠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,锐角△ABC内接于⊙O,若⊙O的半径为6,sinA=
 ,求BC的长.
,求BC的长.
【答案】BC=8.
【解析】试题分析:通过作辅助线构成直角三角形,再利用三角函数知识进行求解.
试题解析:作⊙O的直径CD,连接BD,则CD=2×6=12.
∵

∴

∴


点睛:直径所对的圆周角是直角.
【题型】解答题
【结束】
22【题目】如图,一次函数y=k1x+b与反比例函数y=
 的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式k1x+b>
 的解集;
的解集;(3)若P(p,y1),Q(﹣2,y2)是函数y=
 图象上的两点,且y1≥y2,求实数p的取值范围.
图象上的两点,且y1≥y2,求实数p的取值范围.
相关试题

