【题目】已知,在下列各图中,点O为直线AB上一点,∠AOC=60°,直角三角板的直角顶点放在点处.
(1)如图1,三角板一边OM在射线OB上,另一边ON在直线AB的下方,则∠BOC的度数为°,∠CON的度数为°;
(2)如图2,三角板一边OM恰好在∠BOC的角平分线OE上,另一边ON在直线AB的下方,此时∠BON的度数为°;
(3)请从下列(A),(B)两题中任选一题作答.
我选择: .
(A)在图2中,延长线段NO得到射线OD,如图3,则∠AOD的度数为°;∠DOC与∠BON的数量关系是∠DOC∠BON(填“>”、“=”或“<”);
(B)如图4,MN⊥AB,ON在∠AOC的内部,若另一边OM在直线AB的下方,则∠COM+∠AON的度数为°;∠AOM﹣∠CON的度数为°.
参考答案:
【答案】
(1)120 ;150
(2)30°
(3)A(或B);30;=;150;30
【解析】解:(1)∵∠AOC=60°,∠BOC与∠AOC互补,∠AON=90°
∴∠BOC=180°﹣60°=120°,∠CON=∠AOC+∠AON=60°+90°.
故答案为:120;150.
⑵∵三角板一边OM恰好在∠BOC的角平分线OE上,∠BOC=120°,
∴∠BOM= ![]() ∠BOC=60°,
∠BOC=60°,
又∵∠MON=∠BOM+∠BON=90°,
∴∠BON=90°﹣60°=30°.
故答案为:30°.
⑶(A)∵∠AOD=∠BON(对顶角),∠BON=30°,
∴∠AOD=30°,
又∵∠AOC=60°,
∴∠DOC=∠AOC﹣∠AOD=60°﹣30°=30°=∠BON.
(B)∵MN⊥AB,
∴∠AON与∠MNO互余,
∵∠MNO=60°(三角板里面的60°角),
∴∠AON=90°﹣60°=30°,
∵∠AOC=60°,150
∴∠CON=∠AOC﹣∠AON=60°﹣30°=30°,
∴∠COM+∠AON=∠MON+2∠CON=90°+2×30°=150°,
∠AOM﹣∠CON=∠MON﹣2∠CON=90°﹣2×30°=30°.
故答案为:A(或B);30;=;150;30.
(1)由题意可知∠AON=∠BON=90°,根据邻补角的定义可求出∠BOC的度数;再根据∠CON=∠AOC+∠AON,就可求出结果。
(2)根据题意角平分线的定义可求出∠BOE的度数,再根据∠BON=90°-∠BOE,即可求出结果。
(3)(A)根据对顶角相等得出∠BON=∠AOD,就可求出∠AOD的度数;再求出∠DOC的度数,就可得出结论;
(B)根据已知条件求出∠AOC、∠CON、∠AON的度数,再根据∠COM+∠AON,∠AOM﹣∠CON,即可求出结果。
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两地相距900千米,一列快车从甲地出发匀速开往乙地,速度为120千米/时;快车开出30分钟时,一列慢车从乙地出发匀速开往甲地,速度为90千米/时.设慢车行驶的时间为x小时,快车到达乙地后停止行驶,根据题意解答下列问题:
(1)当快车与慢车相遇时,求慢车行驶的时间;
(2)请从下列(A),(B)两题中任选一题作答.
(A)当两车之间的距离为315千米时,求快车所行的路程;
(B)①在慢车从乙地开往甲地的过程中,求快慢两车之间的距离;(用含x的代数式表示)
我选择: .
作答: -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=6cm,BC=12cm,∠B=90°.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P,Q分别从A,B同时出发,设移动时间为t(s).
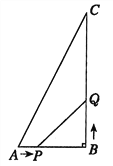
(1)当
 时,求△PBQ的面积;
时,求△PBQ的面积;(2)当
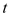 为多少时,四边形APQC的面积最小?最小面积是多少?
为多少时,四边形APQC的面积最小?最小面积是多少?(3)当
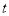 为多少时,△PQB与△ABC相似.
为多少时,△PQB与△ABC相似. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2+6x+5的顶点坐标是________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
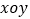 中,已知一次函数
中,已知一次函数 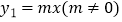 与
与 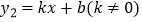 相交于点
相交于点 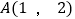 ,且
,且 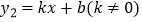 与
与 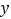 轴交于点
轴交于点  .
.
(1)求一次函数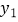 和
和 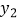 的解析式;
的解析式;
(2)当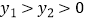 时,求出
时,求出 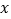 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a3·a4=a12 B. (2a)2=2a2
C. (a3)2=a9 D. (-2×102)3=-8×106
-
科目: 来源: 题型:
查看答案和解析>>【题目】x2﹣10x+ =(x﹣ )2
相关试题

