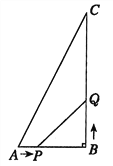
【题目】如图,在△ABC中,AB=6cm,BC=12cm,∠B=90°.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P,Q分别从A,B同时出发,设移动时间为t(s).
(1)当![]() 时,求△PBQ的面积;
时,求△PBQ的面积;
(2)当![]() 为多少时,四边形APQC的面积最小?最小面积是多少?
为多少时,四边形APQC的面积最小?最小面积是多少?
(3)当![]() 为多少时,△PQB与△ABC相似.
为多少时,△PQB与△ABC相似.
参考答案:
【答案】(1)8;(2)当![]() =3时,
=3时,![]() 有最小值27
有最小值27![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】试题分析:(1)根据直角三角形的面积公式和路程=速度×时间进行求解即可;
(2)四边形APQC的面积=△ABC的面积﹣△PBQ的面积,再根据配方法即可求解;
(3)分两种情况讨论:![]() 和
和![]() ,求出对应的t即可.
,求出对应的t即可.
试题解析:(1)当![]() 时,AP=2,BQ=4,PB=4,∴
时,AP=2,BQ=4,PB=4,∴![]() =
=![]() (
(![]() );
);
(2)∵AP=![]() ,BQ=
,BQ=![]() ,PB=
,PB=![]() ,∴
,∴![]() =
= ![]()
=![]() ,∴当
,∴当![]() =3时,
=3时,![]() 有最小值27
有最小值27![]() ;
;
(3)∵△PQB、△ABC是直角三角形,∴由![]() ,即
,即![]() ,解得
,解得![]() ,由
,由![]() ,即
,即![]() ,解得
,解得![]() ,∴当
,∴当![]() 或
或![]() 时,△PQB与△ABC相似.
时,△PQB与△ABC相似.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD是经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠a.

(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图l,若∠BCA=90°,∠a=90°,则BECF;EF|BE﹣AF|(填“>”,“<”或“=”);
②如图(2),若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件 , 使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想(不要求证明). -
科目: 来源: 题型:
查看答案和解析>>【题目】若x2﹣kx+4是一个完全平方式,则k的值是
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两地相距900千米,一列快车从甲地出发匀速开往乙地,速度为120千米/时;快车开出30分钟时,一列慢车从乙地出发匀速开往甲地,速度为90千米/时.设慢车行驶的时间为x小时,快车到达乙地后停止行驶,根据题意解答下列问题:
(1)当快车与慢车相遇时,求慢车行驶的时间;
(2)请从下列(A),(B)两题中任选一题作答.
(A)当两车之间的距离为315千米时,求快车所行的路程;
(B)①在慢车从乙地开往甲地的过程中,求快慢两车之间的距离;(用含x的代数式表示)
我选择: .
作答: -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2+6x+5的顶点坐标是________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在下列各图中,点O为直线AB上一点,∠AOC=60°,直角三角板的直角顶点放在点处.

(1)如图1,三角板一边OM在射线OB上,另一边ON在直线AB的下方,则∠BOC的度数为°,∠CON的度数为°;
(2)如图2,三角板一边OM恰好在∠BOC的角平分线OE上,另一边ON在直线AB的下方,此时∠BON的度数为°;
(3)请从下列(A),(B)两题中任选一题作答.
我选择: .
(A)在图2中,延长线段NO得到射线OD,如图3,则∠AOD的度数为°;∠DOC与∠BON的数量关系是∠DOC∠BON(填“>”、“=”或“<”);
(B)如图4,MN⊥AB,ON在∠AOC的内部,若另一边OM在直线AB的下方,则∠COM+∠AON的度数为°;∠AOM﹣∠CON的度数为°. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
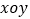 中,已知一次函数
中,已知一次函数 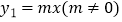 与
与 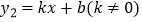 相交于点
相交于点 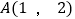 ,且
,且 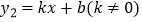 与
与 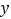 轴交于点
轴交于点  .
.
(1)求一次函数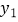 和
和 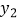 的解析式;
的解析式;
(2)当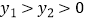 时,求出
时,求出 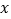 的取值范围.
的取值范围.
相关试题

