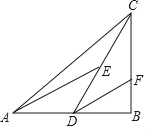
【题目】定义:有两条边长的比值为![]() 的直角三角形叫“潜力三角形”.如图,在△ABC中,∠B=90°,D是AB的中点,E是CD的中点,DF∥AE交BC于点F.
的直角三角形叫“潜力三角形”.如图,在△ABC中,∠B=90°,D是AB的中点,E是CD的中点,DF∥AE交BC于点F.
(1)设“潜力三角形”较短直角边长为a,斜边长为c,请你直接写出![]() 的值为 ;
的值为 ;
(2)若∠AED=∠DCB,求证:△BDF是“潜力三角形”;
(3)若△BDF是“潜力三角形”,且BF=1,求线段AC的长.
参考答案:
【答案】(1)2或![]() ;(2)证明见解析;(3)5或
;(2)证明见解析;(3)5或![]() 或
或![]() 或
或![]() .
.
【解析】试题分析:(1)分两种情况:①当![]() 时,
时,![]() 2;②设另一条直角边长为b,当
2;②设另一条直角边长为b,当![]() 时,b=2a,由勾股定理求出c=
时,b=2a,由勾股定理求出c=![]() ,得出
,得出![]() ;即可得出答案;
;即可得出答案;
(2)延长AE交BC于G,由平行线的性质得出∠AED=∠CDF,BF=GF,再由已知得出∠CDF=∠DCB,证出DF=CF,由平行线得出CG=GF,得出BF=GF=CG,因此DF=CF=2GF=2BF,得出![]() ,即可得出结论;
,即可得出结论;
(3)分四种情况:①当![]() 时;②当
时;②当![]() 时;③当
时;③当![]() 时;④当
时;④当![]() 时;求出BC=3,分别求出AB的长,由勾股定理求出AC即可.
时;求出BC=3,分别求出AB的长,由勾股定理求出AC即可.
试题解析:(1)分两种情况:
①当![]() 时,
时,![]() 2;
2;
②设另一条直角边长为b,当![]() 时,b=2a,
时,b=2a,
∵∠B=90°,
∴c=![]() ,
,
∴![]() ;
;
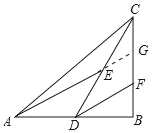
(2)证明:延长AE交BC于G,如图所示:
∵DF∥AE,D是AB的中点,
∴∠AED=∠CDF,BF=GF,
∵∠AED=∠DCB,
∴∠CDF=∠DCB,
∴DF=CF,
∵DF∥AE,E是CD的中点,
∴CG=GF,
∴BF=GF=CG,
∴DF=CF=2GF=2BF,
∴![]() ,
,
又∵∠B=90°,
∴△BDF是“潜力三角形”;
(3)延长AE交BC于G,如图所示.

分四种情况:
①当![]() 时,
时,
∵BF=1,
∴GF=CG=BF=1,BD=2,
∴AB=2BD=4,BC=3,
∴AC=![]() ;
;
②当![]() 时,DF=2BF=2,
时,DF=2BF=2,
∴BD=![]()
∴AB=2BD=2![]() ,
,
∵BC=3,∠B=90°,
∴AC=![]() ;
;
③当![]() 时,BD=
时,BD=![]() BF=
BF=![]() ,
,
∴AB=2BD=1,
∵BC=3,∠B=90°,
∴AC=![]() ;
;
④当![]() 时,
时,
设BD=x,则DF=2x,
由勾股定理得:(2x)2﹣x2=12,
解得:x=![]() ,
,
∴AB=2BD=![]() ,
,
∵BC=3,∠B=90°,
∴AC=![]() ;
;
综上所述:若△BDF是“潜力三角形”,且BF=1,线段AC的长为5或![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E、F在AC上,且AF=CE,点G、H分别在AB、CD上,且AG=CH,AC与GH相交于点O.
(1)求证:EG//FH;
(2)GH、EF互相平分.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知P为⊙O外一点,PA、PB分别切⊙O于A、B两点,点C为⊙O上一点.
(1)如图1,若AC为直径,求证:OP∥BC;
(2)如图2,若sin∠P=
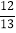 ,求tanC的值.
,求tanC的值.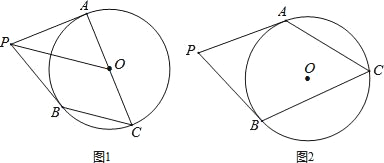
-
科目: 来源: 题型:
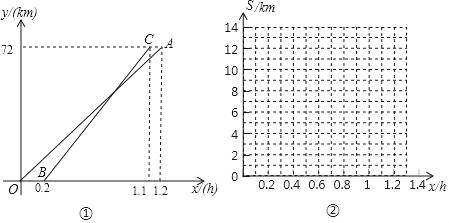
查看答案和解析>>【题目】甲、乙两人周末从同一地点出发去某景点,因乙临时有事,甲坐地铁先出发,甲出发0.2小时后乙开汽车前往.设甲行驶的时间为x(h),甲、乙两人行驶的路程分别为y1(km)与y2(km).如图①是y1与y2关于x的函数图象.
(1)分别求线段OA与线段BC所表示的y1与y2关于x的函数表达式;
(2)当x为多少时,两人相距6km?
(3)设两人相距S千米,在图②所给的直角坐标系中画出S关于x的函数图象.
-
科目: 来源: 题型:
查看答案和解析>>【题目】统计七年级部分同学的跳高测试成绩,得到如下频率直方图(每组含前一个边界值,不含后一个边界值).

(1)参加测试的总人数是多少人?
(2)组距为多少?
(3)跳高成绩在
 (含
(含 )以上的有多少人?占总人数的百分之几?
)以上的有多少人?占总人数的百分之几? -
科目: 来源: 题型:
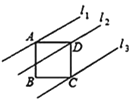
查看答案和解析>>【题目】如图,直线l1,l2,l3分别过正方形ABCD的三个顶点A,D,C,且相互平行,若l1,l2的距离为2,l2,l3的距离为4,则正方形的对角线长为_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若抛物线L:y=ax2+bx+c(a,b,c是常数,abc≠0)与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系.此时,直线l叫做抛物线L的“带线”,抛物线L叫做直线l的“路线”.
(1)若直线y=mx+1与抛物线y=x2﹣2x+n具有“一带一路”关系,求m,n的值;
(2)若某“路线”L的顶点在反比例函数y=
 的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;
的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;(3)当常数k满足
 ≤k≤2时,求抛物线L:y=ax2+(3k2﹣2k+1)x+k的“带线”l与x轴,y轴所围成的三角形面积的取值范围.
≤k≤2时,求抛物线L:y=ax2+(3k2﹣2k+1)x+k的“带线”l与x轴,y轴所围成的三角形面积的取值范围.
相关试题

