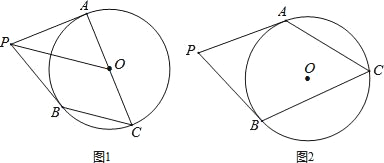
【题目】已知P为⊙O外一点,PA、PB分别切⊙O于A、B两点,点C为⊙O上一点.
(1)如图1,若AC为直径,求证:OP∥BC;
(2)如图2,若sin∠P=![]() ,求tanC的值.
,求tanC的值.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连接AB交PO于M,根据切线性质得出PA=PB,OP平分∠APB,推出∠AMO=90°,根据平行线的判定推出即可;
(2)求出∠E=∠C,求出∠E=∠PBA,解直角三角形求出即可.
试题解析:(1)证明:连接AB交PO于M,
∵PA、PB分别切⊙O于A、B两点,
∴PA=PB,OP平分∠APB,
∴AB⊥OP,
∴∠AMO=90°,
∵AC为直径,
∴∠ABC=90°,
∴∠AMO=∠ABC,
∴OP∥BC;
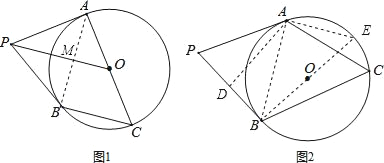
(2)连接AB,过A作AD⊥PB于D,作直径BE,连接AE,
∵PB为⊙O的切线,
∴BE⊥PB,
∴∠PBA+∠ABE=90°,
∵BE为直径,
∴∠BAE=90°,
∴∠E+∠ABE=90°,
∴∠E=∠ABP,
∵∠E=∠C,
∴∠C=∠ABP,
∵sin∠P=![]() ,
,
∴设AD=12x,则PA=13x,PD=5x,
∴BD=8x,
∴tan∠ABD=![]() ,
,
∴tan∠C=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
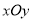 中,对于任意一点
中,对于任意一点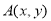 ,定义点
,定义点 的“离心值”
的“离心值”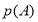 为:
为: 时,例如对于点
时,例如对于点 ,因为
,因为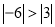 ,所以
,所以 .
.解决下列问题:
(1)已知
 ,
,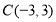 ,
,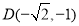 ,直接写出
,直接写出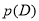 的值,并将
的值,并将 ,
,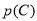 ,
,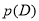 按从小到大的顺序排列(用“<”连接);
按从小到大的顺序排列(用“<”连接);(2)如图,点
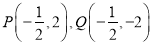 ,线段
,线段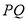 上的点
上的点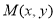 ,
,①若
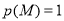 ,求点
,求点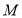 的坐标;
的坐标;②在图中画出满足
 的点
的点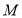 组成的图形,并用语言描述该图形的特征;
组成的图形,并用语言描述该图形的特征;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.

(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E、F在AC上,且AF=CE,点G、H分别在AB、CD上,且AG=CH,AC与GH相交于点O.
(1)求证:EG//FH;
(2)GH、EF互相平分.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人周末从同一地点出发去某景点,因乙临时有事,甲坐地铁先出发,甲出发0.2小时后乙开汽车前往.设甲行驶的时间为x(h),甲、乙两人行驶的路程分别为y1(km)与y2(km).如图①是y1与y2关于x的函数图象.
(1)分别求线段OA与线段BC所表示的y1与y2关于x的函数表达式;
(2)当x为多少时,两人相距6km?
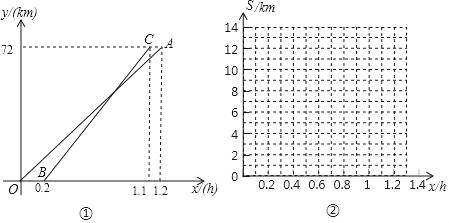
(3)设两人相距S千米,在图②所给的直角坐标系中画出S关于x的函数图象.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:有两条边长的比值为
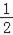 的直角三角形叫“潜力三角形”.如图,在△ABC中,∠B=90°,D是AB的中点,E是CD的中点,DF∥AE交BC于点F.
的直角三角形叫“潜力三角形”.如图,在△ABC中,∠B=90°,D是AB的中点,E是CD的中点,DF∥AE交BC于点F.(1)设“潜力三角形”较短直角边长为a,斜边长为c,请你直接写出
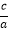 的值为 ;
的值为 ;(2)若∠AED=∠DCB,求证:△BDF是“潜力三角形”;
(3)若△BDF是“潜力三角形”,且BF=1,求线段AC的长.
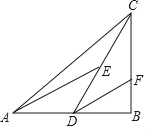
-
科目: 来源: 题型:
查看答案和解析>>【题目】统计七年级部分同学的跳高测试成绩,得到如下频率直方图(每组含前一个边界值,不含后一个边界值).

(1)参加测试的总人数是多少人?
(2)组距为多少?
(3)跳高成绩在
 (含
(含 )以上的有多少人?占总人数的百分之几?
)以上的有多少人?占总人数的百分之几?
相关试题

