【题目】若抛物线L:y=ax2+bx+c(a,b,c是常数,abc≠0)与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系.此时,直线l叫做抛物线L的“带线”,抛物线L叫做直线l的“路线”.
(1)若直线y=mx+1与抛物线y=x2﹣2x+n具有“一带一路”关系,求m,n的值;
(2)若某“路线”L的顶点在反比例函数y=![]() 的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;
的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;
(3)当常数k满足![]() ≤k≤2时,求抛物线L:y=ax2+(3k2﹣2k+1)x+k的“带线”l与x轴,y轴所围成的三角形面积的取值范围.
≤k≤2时,求抛物线L:y=ax2+(3k2﹣2k+1)x+k的“带线”l与x轴,y轴所围成的三角形面积的取值范围.
参考答案:
【答案】(1)m的值为﹣1,n的值为1.(2)y=2(x+1)2﹣6或y=﹣![]() (x﹣3)2+2.(3)
(x﹣3)2+2.(3)![]() ≤S≤
≤S≤![]() .
.
【解析】
试题分析:(1)确定直线y=mx+1与y轴的交点坐标,将其代入抛物线解析式中即可求出n的值;再根据抛物线的解析式找出顶点坐标,将其代入直线解析式中即可得出结论;(2)确定直线与反比例函数图象的交点坐标,由此设出抛物线的解析式,再由直线的解析式找出直线与x轴的交点坐标,将其代入抛物线解析式中即可得出结论;(3)由抛物线解析式找出抛物线与y轴的交点坐标,再根据抛物线的解析式找出其顶点坐标,由两点坐标结合待定系数法即可得出与该抛物线对应的“带线”l的解析式,找出该直线与x、y轴的交点坐标,结合三角形的面积找出面积S关于k的关系上,由二次函数的性质即可得出结论.
试题解析:(1)令直线y=mx+1中x=0,则y=1,
即直线与y轴的交点为(0,1);
将(0,1)代入抛物线y=x2﹣2x+n中,
得n=1.
∵抛物线的解析式为y=x2﹣2x+1=(x﹣1)2,
∴抛物线的顶点坐标为(1,0).
将点(1,0)代入到直线y=mx+1中,
得:0=m+1,解得:m=﹣1.
答:m的值为﹣1,n的值为1.
(2)将y=2x﹣4代入到y=![]() 中有,
中有,
2x﹣4=![]() ,即2x2﹣4x﹣6=0,
,即2x2﹣4x﹣6=0,
解得:x1=﹣1,x2=3.
∴该“路线”L的顶点坐标为(﹣1,﹣6)或(3,2).
令“带线”l:y=2x﹣4中x=0,则y=﹣4,
∴“路线”L的图象过点(0,﹣4).
设该“路线”L的解析式为y=m(x+1)2﹣6或y=n(x﹣3)2+2,
由题意得:﹣4=m(0+1)2﹣6或﹣4=n(0﹣3)2+2,
解得:m=2,n=﹣![]() .
.
∴此“路线”L的解析式为y=2(x+1)2﹣6或y=﹣![]() (x﹣3)2+2.
(x﹣3)2+2.
(3)令抛物线L:y=ax2+(3k2﹣2k+1)x+k中x=0,则y=k,
即该抛物线与y轴的交点为(0,k).
抛物线L:y=ax2+(3k2﹣2k+1)x+k的顶点坐标为(﹣![]() ,
,![]() ),
),
设“带线”l的解析式为y=px+k,
∵点(﹣![]() ,
,![]() )在y=px+k上,
)在y=px+k上,
∴![]() =﹣p
=﹣p![]() +k,
+k,
解得:p=![]() .
.
∴“带线”l的解析式为y=![]() x+k.
x+k.
令∴“带线”l:y=![]() x+k中y=0,则0=
x+k中y=0,则0=![]() x+k,
x+k,
解得:x=﹣![]() .
.
即“带线”l与x轴的交点为(﹣![]() ,0),与y轴的交点为(0,k).
,0),与y轴的交点为(0,k).
∴“带线”l与x轴,y轴所围成的三角形面积S=![]() |﹣
|﹣![]() |×|k|,
|×|k|,
∵![]() ≤k≤2,
≤k≤2,
∴![]() ≤
≤![]() ≤2,
≤2,
∴S=![]() =
=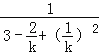 =
=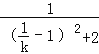 ,
,
当![]() =1时,S有最大值,最大值为
=1时,S有最大值,最大值为![]() ;
;
当![]() =2时,S有最小值,最小值为
=2时,S有最小值,最小值为![]() .
.
故抛物线L:y=ax2+(3k2﹣2k+1)x+k的“带线”l与x轴,y轴所围成的三角形面积的取值范围为![]() ≤S≤
≤S≤![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O是正方形ABCD两对角线的交点. 分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.
(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转
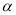 角(0°<
角(0°< 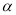 <360°)得到正方形
<360°)得到正方形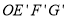 ,如图2.
,如图2.①在旋转过程中,当∠
 是直角时,求
是直角时,求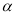 的度数;(注明:当直角边为斜边一半时,这条直角边所对的锐角为30度)
的度数;(注明:当直角边为斜边一半时,这条直角边所对的锐角为30度)②若正方形ABCD的边长为1,在旋转过程中,求
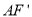 长的最大值和此时
长的最大值和此时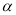 的度数,直接写出结果不必说明理由.
的度数,直接写出结果不必说明理由.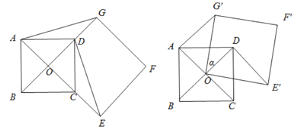
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.
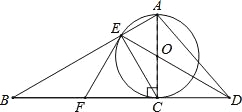
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2m,台阶AC的坡度为1:
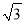 ,且B,C,E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽略不计).
,且B,C,E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽略不计).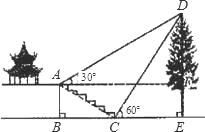
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=x2+2x﹣1
(1)用配方法或公式法求出它的顶点坐标和对称轴.
(2)直接写出它与y轴的交点坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空:单项式2.7×103a2b的系数是________,次数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中:①因为∠1与∠2是对顶角,所以∠1=∠2;②因为∠1与∠2是邻补角,所以∠1=∠2;③因为∠1与∠2不是对顶角,所以∠1≠∠2;④因为∠1与∠2不是邻补角,所以∠1+∠2≠180°.
其中正确的有__________
相关试题

