【题目】某初中要调查学校学生(总数 1000 人)双休日课外阅读情况,随机调查了一部分学生,调查得 到的数据分别制成频数直方图(如图 1)和扇形统计图(如图 2).

(1)请补全上述统计图(直接填在图中);
(2) 试确定这个样本的中位数和众数;
(3)请估计该学校 1000 名学生双休日课外阅读时间不少于 4 小时的人数.
参考答案:
【答案】(1)画图见解析;(2)中位数是3小时,众数是4小时;(3)400人.
【解析】
(1)根据阅读5小时以上频数为6,所占百分比为12%,求出数据的总数,再用数据总数减去其余各组频数得到阅读3小时以上频数,然后补全频数分布直方图,分别求得阅读0小时和4小时的人数所占百分比,补全扇形图;
(2)利用各组频数和总数之间的关系确定中位数和众数;
(3)用1000乘以每周课外阅读时间不小于4小时的学生所占百分比即可.
解:(1)总人数:6![]() 12%= 50 (人),
12%= 50 (人),
阅读3小时以上人数:50-4-6-8-14-6= 12 (人),
阅读3小时以上人数的百分比为12![]() 50= 24% ,
50= 24% ,
阅读0小时以上人数的百分比为4![]() 50= 8% .
50= 8% .
图如下:

(2)中位数是3小时,众数是4小时;
(3) 1000![]() (28% + 12%)
(28% + 12%)
= 1000![]() 40%
40%
= 400(人)
答:该学校1000名学生双休日课外阅读时间不少于4小时的人数为400人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
关于
 的方程:
的方程: 的解为:
的解为:  ,
, 
 (可变形为
(可变形为 )的解为:
)的解为:  ,
, 
 的解为:
的解为:  ,
, 
 的解为:
的解为:  ,
, 
…………
根据以上材料解答下列问题:
(1)①方程
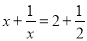 的解为 .
的解为 .②方程
 的解为 .
的解为 .(2)解关于
 方程:
方程:①
 (
( )
)②
 (
( )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于
 MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D. 下列结论:①AD是∠BAC的平分线;②点D在AB的垂直平分线上;③∠ADC=60°;④
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D. 下列结论:①AD是∠BAC的平分线;②点D在AB的垂直平分线上;③∠ADC=60°;④ 。其中正确的结论有( )
。其中正确的结论有( )
A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC 是ABCD 的一条对角线,BE⊥AC,DF⊥AC,垂足分别为 E,F.

(1)求证:△ADF≌△CBE;
(2)求证:四边形 DFBE 是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
 与x轴交于B(-3,0)、C(1,0)两点,与y轴交于点A(0,2),抛物线的顶点为D.连接AB,点E是第二象限内的抛物线上的一动点,过点E作EP⊥BC于点P,交线段AB于点F.
与x轴交于B(-3,0)、C(1,0)两点,与y轴交于点A(0,2),抛物线的顶点为D.连接AB,点E是第二象限内的抛物线上的一动点,过点E作EP⊥BC于点P,交线段AB于点F.(1)求此抛物线的解析式;
(2)过点E作EG⊥AB于点G,Q为线段AC的中点,当△EGF周长最大时,在
 轴上找一点R,使得|RE-RQ|值最大,请求出R点的坐标及|RE-RQ|的最大值;
轴上找一点R,使得|RE-RQ|值最大,请求出R点的坐标及|RE-RQ|的最大值;
(3)在(2)的条件下,将△PED绕E点旋转得△ED′P′,当△AP′P是以AP为直角边的直角三角形时,求点P′的坐标.

-
科目: 来源: 题型:
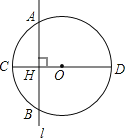
查看答案和解析>>【题目】如图,⊙O的半径OC=10cm,直线l⊥CO,垂足为H,交⊙O于A,B两点,AB=16cm,直线l平移多少厘米时能与⊙O相切?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程:x
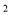 ﹣2x﹣8=0,解决一下问题:
﹣2x﹣8=0,解决一下问题:(1)不解方程判断此方程的根的情况;
(2)请按要求分别解这个方程:①配方法;②因式分解法.
(3)这些方法都是将解 转化为解 ;
(4)尝试解方程:
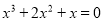 .
.
相关试题

