【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D. 下列结论:①AD是∠BAC的平分线;②点D在AB的垂直平分线上;③∠ADC=60°;④
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D. 下列结论:①AD是∠BAC的平分线;②点D在AB的垂直平分线上;③∠ADC=60°;④![]() 。其中正确的结论有( )
。其中正确的结论有( )

A. 1B. 2C. 3D. 4
参考答案:
【答案】D
【解析】
①根据作图的过程可以判定AD是∠BAC的角平分线;
②利用等角对等边可以证得△ADB的等腰三角形,由等腰三角形的“三合一”的性质可以证明点D在AB的垂直平分线上;
③利用角平分线的定义可以推知∠CAD=30°,则由直角三角形的性质来求∠ADC的度数;
④利用30度角所对的直角边是斜边的一半、三角形的面积计算公式来求两个三角形的面积之比.
解:如图:
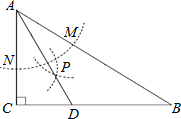
根据作图方法可得AD是∠BAC的平分线,故①正确;
∵∠C=90°,∠B=30°,
∴∠CAB=60°,
∵AD是∠BAC的平分线,
∴∠DAC=∠DAB=30°,
∵∠B=30°,∠DAB=30°,
∴AD=DB,
∴点D在AB的中垂线上,故②正确;
∴∠ADC=60°,故③正确;
∵∠CAD=30°,
![]()
∵AD=DB,
![]()
∴![]()
故④正确。
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为矩形,连接BD,AB=2AD,点E在AB边上,连接ED.
(1)若∠ADE=30°,DE=6,求△BDE的面积;
(2)延长CB至点F使得BF=2AD,连接FE并延长交AD于点M,过点A作AN⊥EM于点N,连接BN,求证:FN=AN+
 BN.
BN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个正方形内两个相邻正方形的面积分别为 4 和 2,它们都有两个顶点在大正方形的边 上且组成的图形为轴对称图形,则图中阴影部分的面积为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
关于
 的方程:
的方程: 的解为:
的解为:  ,
, 
 (可变形为
(可变形为 )的解为:
)的解为:  ,
, 
 的解为:
的解为:  ,
, 
 的解为:
的解为:  ,
, 
…………
根据以上材料解答下列问题:
(1)①方程
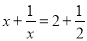 的解为 .
的解为 .②方程
 的解为 .
的解为 .(2)解关于
 方程:
方程:①
 (
( )
)②
 (
( )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC 是ABCD 的一条对角线,BE⊥AC,DF⊥AC,垂足分别为 E,F.

(1)求证:△ADF≌△CBE;
(2)求证:四边形 DFBE 是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某初中要调查学校学生(总数 1000 人)双休日课外阅读情况,随机调查了一部分学生,调查得 到的数据分别制成频数直方图(如图 1)和扇形统计图(如图 2).

(1)请补全上述统计图(直接填在图中);
(2) 试确定这个样本的中位数和众数;
(3)请估计该学校 1000 名学生双休日课外阅读时间不少于 4 小时的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
 与x轴交于B(-3,0)、C(1,0)两点,与y轴交于点A(0,2),抛物线的顶点为D.连接AB,点E是第二象限内的抛物线上的一动点,过点E作EP⊥BC于点P,交线段AB于点F.
与x轴交于B(-3,0)、C(1,0)两点,与y轴交于点A(0,2),抛物线的顶点为D.连接AB,点E是第二象限内的抛物线上的一动点,过点E作EP⊥BC于点P,交线段AB于点F.(1)求此抛物线的解析式;
(2)过点E作EG⊥AB于点G,Q为线段AC的中点,当△EGF周长最大时,在
 轴上找一点R,使得|RE-RQ|值最大,请求出R点的坐标及|RE-RQ|的最大值;
轴上找一点R,使得|RE-RQ|值最大,请求出R点的坐标及|RE-RQ|的最大值;
(3)在(2)的条件下,将△PED绕E点旋转得△ED′P′,当△AP′P是以AP为直角边的直角三角形时,求点P′的坐标.

相关试题

