【题目】如图,曲线l是由函数y= ![]() 在第一象限内的图象绕坐标原点O逆时针旋转45°得到的,过点A(﹣4
在第一象限内的图象绕坐标原点O逆时针旋转45°得到的,过点A(﹣4 ![]() ,4
,4 ![]() ),B(2
),B(2 ![]() ,2
,2 ![]() )的直线与曲线l相交于点M、N,则△OMN的面积为 .
)的直线与曲线l相交于点M、N,则△OMN的面积为 . 
参考答案:
【答案】8
【解析】解:∵A(﹣4 ![]() ,4
,4 ![]() ),B(2
),B(2 ![]() ,2
,2 ![]() ),
),
∴OA⊥OB,
建立如图新的坐标系(OB为x′轴,OA为y′轴.
在新的坐标系中,A(0,8),B(4,0),
∴直线AB解析式为y′=﹣2x′+8,
由  ,解得
,解得 ![]() 或
或 ![]() ,
,
∴M(1.6),N(3,2),
∴S△OMN=S△OBM﹣S△OBN= ![]() 46﹣
46﹣ ![]() 42=8,
42=8,
所以答案是8
【考点精析】解答此题的关键在于理解比例系数k的几何意义的相关知识,掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:以直线AB上一点O为端点作射线OM、ON,将一个直角三角形的直角顶点放在O处(∠COD=90°).
(1)如图1,直角三角板COD的边OD放在射线OB上,OM平分∠AOC,ON和OB重合,则∠MON=_°;
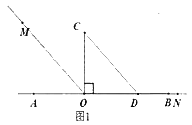
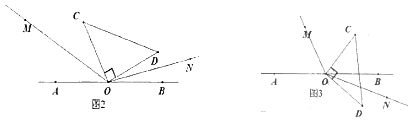
(2)直角三角板COD绕点O旋转到如图2的位置,OM平分∠AOC,ON平分∠BOD,求∠MON的度数。
(3)直角三角板COD绕点O旋转到如图3的位置,OM平分∠ AOC ,ON平分∠BOD,猜想∠MON的度数,并说明理由。
-
科目: 来源: 题型:
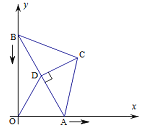
查看答案和解析>>【题目】如图,在△ABC中,BC=AC=5,AB=8,CD为AB边的高,点A在x轴上,点B在y轴上,点C在第一象限,若A从原点出发,沿x轴向右以每秒4个单位长的速度运动,则点B随之沿y轴下滑,并带动△ABC在平面内滑动,设运动时间为t秒,当B到达原点时停止运动.当△ABC的边与坐标轴平行时,t=_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,点E在△ABC外一点,CE⊥AE于点E,CE=
 BC.
BC.(1)作出△ABC的角平分线AD.(要求:尺规作图,不写作法,保留作图痕迹.)
(2)求证:∠ACE=∠B.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. =±5
=±5
B.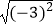 =﹣3
=﹣3
C.±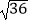 =±6
=±6
D.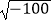 =﹣10
=﹣10 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A是反比例函数y=﹣
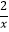 的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为 .
的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为 . 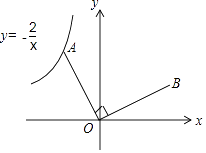
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
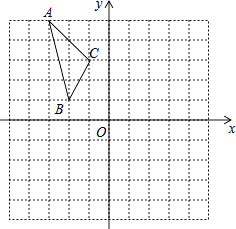
①若△ABC经过平移后得到△A1B1C1 , 已知点C1的坐标为(4,0),写出顶点A1 , B1的坐标;
②若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
③将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3 , 写出△A3B3C3的各顶点的坐标.
相关试题

