【题目】已知:如图,在△ABC中,AB=AC,点E在△ABC外一点,CE⊥AE于点E,CE=![]() BC.
BC.
(1)作出△ABC的角平分线AD.(要求:尺规作图,不写作法,保留作图痕迹.)
(2)求证:∠ACE=∠B.

参考答案:
【答案】(1)详见解析;(2)详见解析.
【解析】
第一问根据角平分线的作图步骤,先以A为圆心任意长为半径交AB、AC于两个点,再分别以这两个点为圆心,以大于这两点距离一半的长度为半径画圆弧,圆弧交点与点A连线所在的直线就是角平分线;
第二问由角平分线性质得到BD=CE,再证明两个三角形全等,进而得到角相等.
解:(1)如图所示,AD即为所求.

(2)∵AB=AC,AD平分∠BAC,
∴AD⊥BC,BD=CD=![]() BC,
BC,
∵CE=![]() BC,
BC,
∴BD=CE,
在Rt△ABD和Rt△ACE中
∵![]() ,
,
∴Rt△ABD≌Rt△ACE(HL)
∴∠B=∠ACE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,
实验次数
100
200
300
500
800
1000
2000
频率
0.365
0.328
0.330
0.334
0.336
0.332
0.333
则符合这一结果的实验最有可能的是( )
A.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是梅花
B.抛一枚硬币,出现反面的概率
C.袋子里有除了颜色都一样3个红球,2个白球,随机摸一个球是白球的概率
D.抛一个质地均匀的正六面体骰子,向上的面点数大于4
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:以直线AB上一点O为端点作射线OM、ON,将一个直角三角形的直角顶点放在O处(∠COD=90°).
(1)如图1,直角三角板COD的边OD放在射线OB上,OM平分∠AOC,ON和OB重合,则∠MON=_°;
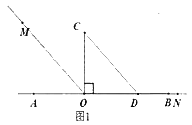
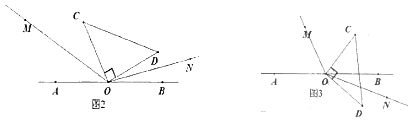
(2)直角三角板COD绕点O旋转到如图2的位置,OM平分∠AOC,ON平分∠BOD,求∠MON的度数。
(3)直角三角板COD绕点O旋转到如图3的位置,OM平分∠ AOC ,ON平分∠BOD,猜想∠MON的度数,并说明理由。
-
科目: 来源: 题型:
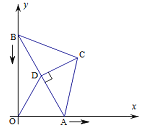
查看答案和解析>>【题目】如图,在△ABC中,BC=AC=5,AB=8,CD为AB边的高,点A在x轴上,点B在y轴上,点C在第一象限,若A从原点出发,沿x轴向右以每秒4个单位长的速度运动,则点B随之沿y轴下滑,并带动△ABC在平面内滑动,设运动时间为t秒,当B到达原点时停止运动.当△ABC的边与坐标轴平行时,t=_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,曲线l是由函数y=
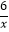 在第一象限内的图象绕坐标原点O逆时针旋转45°得到的,过点A(﹣4
在第一象限内的图象绕坐标原点O逆时针旋转45°得到的,过点A(﹣4 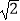 ,4
,4 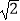 ),B(2
),B(2 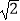 ,2
,2 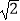 )的直线与曲线l相交于点M、N,则△OMN的面积为 .
)的直线与曲线l相交于点M、N,则△OMN的面积为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. =±5
=±5
B.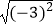 =﹣3
=﹣3
C.±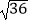 =±6
=±6
D.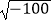 =﹣10
=﹣10 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A是反比例函数y=﹣
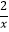 的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为 .
的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为 . 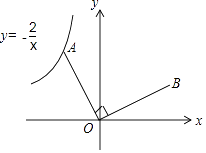
相关试题

