【题目】问题情境:以直线AB上一点O为端点作射线OM、ON,将一个直角三角形的直角顶点放在O处(∠COD=90°).
(1)如图1,直角三角板COD的边OD放在射线OB上,OM平分∠AOC,ON和OB重合,则∠MON=_°;
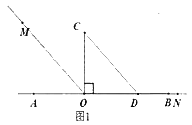
(2)直角三角板COD绕点O旋转到如图2的位置,OM平分∠AOC,ON平分∠BOD,求∠MON的度数。
(3)直角三角板COD绕点O旋转到如图3的位置,OM平分∠ AOC ,ON平分∠BOD,猜想∠MON的度数,并说明理由。
参考答案:
【答案】(1)135;
(2)∠MON=135°
(3)猜想∠MON=135°,证明见解析.
【解析】
(1)先求出∠COM=45°,再利用∠MON=∠COM+∠CON即可求出;
(2)先求出∠AOC+∠BOD=90°,再根据OM平分∠AOC,ON平分∠BOD,可知∠COM+∠DON=45°,再利用∠MON=∠COM+∠DON+∠COD即可求出;
(3)如图延长NO至Q、DO至H,则∠DOH为平角,∠COH=90°,根据对顶角相等,知∠BOD=∠AOH,∠NOD=∠QOH,再根据∠COH=∠AOC-∠AOH=90°,又OM平分∠AOC,ON平分∠BOD,得∠COM-∠QOH=45°,则∠MON=∠COD-∠NOD+∠COM=∠COD+∠COM-∠QOH=90°+45°=135°.
(1)∵∠AOC=90°,OM平分∠AOC,
∴∠COM=45°,
∴∠MON=∠COM+∠CON=45°+90°=135°;
(2)∵∠COD=90°,
∴∠AOC+∠BOD=90°,
∵OM平分∠AOC,ON平分∠BOD,
∴∠COM+∠DON=![]() (∠AOC+∠BOD)=45°,
(∠AOC+∠BOD)=45°,
∴∠MON=∠COM+∠DON+∠COD=45°+90°=135°;
(3)猜想∠MON=135°,证明如下:
如图延长NO至Q、DO至H,
则∠DOH为平角,∠COH=90°,
∴∠COH=∠AOC-∠AOH=90°,
又∵∠BOD=∠AOH,∠NOD=∠QOH,
OM平分∠AOC,ON平分∠BOD,
∴∠COM-∠QOH=45°,
则∠MON=∠COD-∠NOD+∠COM
=∠COD+∠COM-∠QOH
=90°+45°=135°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校在一次环保知识宣传活动中,需要印刷若干份调查问卷。印刷厂有甲、乙两种收费方式:甲种方式收制版费6元,每一份收印刷费0.1元;乙种方式不收制版费,每印一份收印刷费0.12元。设共印调查问卷
 份:
份:(1)按甲种方式应收费多少元,按乙种方式应收费多少元(用含
 的代数式表示);
的代数式表示);(2)若共需印刷500份调查问卷,通过计算说明选用哪种方式合算?
(3)印刷多少份调查问卷时,甲、乙两种方式收费一样多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、F、C、E在一条直线上,AC=DF,BF=CE,那么添加下列一个条件后,仍无法判断△ABC≌△DEF的是( )
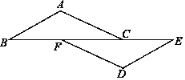
A. ∠A=∠D=90° B. ∠BCA=∠EFD C. ∠B=∠E D. AB=DE
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,
实验次数
100
200
300
500
800
1000
2000
频率
0.365
0.328
0.330
0.334
0.336
0.332
0.333
则符合这一结果的实验最有可能的是( )
A.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是梅花
B.抛一枚硬币,出现反面的概率
C.袋子里有除了颜色都一样3个红球,2个白球,随机摸一个球是白球的概率
D.抛一个质地均匀的正六面体骰子,向上的面点数大于4
-
科目: 来源: 题型:
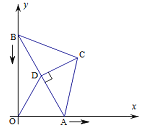
查看答案和解析>>【题目】如图,在△ABC中,BC=AC=5,AB=8,CD为AB边的高,点A在x轴上,点B在y轴上,点C在第一象限,若A从原点出发,沿x轴向右以每秒4个单位长的速度运动,则点B随之沿y轴下滑,并带动△ABC在平面内滑动,设运动时间为t秒,当B到达原点时停止运动.当△ABC的边与坐标轴平行时,t=_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,点E在△ABC外一点,CE⊥AE于点E,CE=
 BC.
BC.(1)作出△ABC的角平分线AD.(要求:尺规作图,不写作法,保留作图痕迹.)
(2)求证:∠ACE=∠B.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,曲线l是由函数y=
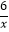 在第一象限内的图象绕坐标原点O逆时针旋转45°得到的,过点A(﹣4
在第一象限内的图象绕坐标原点O逆时针旋转45°得到的,过点A(﹣4 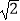 ,4
,4 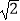 ),B(2
),B(2 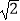 ,2
,2 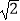 )的直线与曲线l相交于点M、N,则△OMN的面积为 .
)的直线与曲线l相交于点M、N,则△OMN的面积为 . 
相关试题

