【题目】如图,抛物线y= ![]() x2+bx+c经过点B(3,0),C(0,﹣2),直线l:y=﹣
x2+bx+c经过点B(3,0),C(0,﹣2),直线l:y=﹣ ![]() x﹣
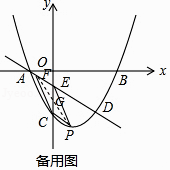
x﹣ ![]() 交y轴于点E,且与抛物线交于A,D两点,P为抛物线上一动点(不与A,D重合).
交y轴于点E,且与抛物线交于A,D两点,P为抛物线上一动点(不与A,D重合).
(1)求抛物线的解析式;
(2)当点P在直线l下方时,过点P作PM∥x轴交l于点M,PN∥y轴交l于点N,求PM+PN的最大值.
(3)设F为直线l上的点,以E,C,P,F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
参考答案:
【答案】
(1)
解:把B(3,0),C(0,﹣2)代入y= ![]() x2+bx+c得,
x2+bx+c得, 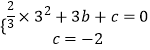 ,
,
∴ 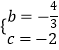
∴抛物线的解析式为:y= ![]() x2﹣
x2﹣ ![]() x﹣2
x﹣2
(2)
解:设P(m, ![]() m2﹣
m2﹣ ![]() m﹣2),
m﹣2),
∵PM∥x轴,PN∥y轴,M,N在直线AD上,
∴N(m,﹣ ![]() m﹣
m﹣ ![]() ),M(﹣m2+2m+2,
),M(﹣m2+2m+2, ![]() m2﹣
m2﹣ ![]() m﹣2),
m﹣2),
∴PM+PN=﹣m2+2m+2﹣m﹣ ![]() m﹣
m﹣ ![]() ﹣
﹣ ![]() m2+
m2+ ![]() m+2=﹣
m+2=﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() =﹣
=﹣ ![]() (m﹣
(m﹣ ![]() )2+
)2+ ![]() ,
,
∴当m= ![]() 时,PM+PN的最大值是
时,PM+PN的最大值是 ![]()
(3)
解:能,
理由:∵y=﹣ ![]() x﹣
x﹣ ![]() 交y轴于点E,
交y轴于点E,
∴E(0,﹣ ![]() ),
),
∴CE= ![]() ,
,
设P(m, ![]() m2﹣
m2﹣ ![]() m﹣2),
m﹣2),
∵以E,C,P,F为顶点的四边形能否构成平行四边形,
①以CE为边,∴CE∥PF,CE=PF,
∴F(m,﹣ ![]() m﹣
m﹣ ![]() ),
),
∴﹣ ![]() m﹣
m﹣ ![]() ﹣
﹣ ![]() m2+
m2+ ![]() m+2=
m+2= ![]() ,
,
∴m=1,m=0(舍去),
②以CE为对角线,连接PF交CE于G,
∴CG=GE,PG=FG,
∴G(0,﹣ ![]() ),
),
设P(m, ![]() m2﹣
m2﹣ ![]() m﹣2),则F(﹣m,
m﹣2),则F(﹣m, ![]() m﹣
m﹣ ![]() ),
),
∴ ![]() ×(
×( ![]() m2﹣
m2﹣ ![]() m﹣2+
m﹣2+ ![]() m﹣
m﹣ ![]() )=﹣
)=﹣ ![]() ,
,
∵△<0,
∴此方程无实数根,
综上所述,当m=1时,以E,C,P,F为顶点的四边形能否构成平行四边形.
【解析】(1.)把B(3,0),C(0,﹣2)代入y= ![]() x2+bx+c解方程组即可得到结论;(2.)设P(m,
x2+bx+c解方程组即可得到结论;(2.)设P(m, ![]() m2﹣
m2﹣ ![]() m﹣2),得到N(m,﹣
m﹣2),得到N(m,﹣ ![]() m﹣
m﹣ ![]() ),M(﹣m2+2m+2,
),M(﹣m2+2m+2, ![]() m2﹣
m2﹣ ![]() m﹣2),根据二次函数的性质即可得到结论;
m﹣2),根据二次函数的性质即可得到结论;
(3.)求得E(0,﹣ ![]() ),得到CE=
),得到CE= ![]() ,设P(m,
,设P(m, ![]() m2﹣
m2﹣ ![]() m﹣2),①以CE为边,根据CE=PF,列方程得到m=1,m=0(舍去),②以CE为对角线,连接PF交CE于G,CG=GE,PG=FG,得到G(0,﹣
m﹣2),①以CE为边,根据CE=PF,列方程得到m=1,m=0(舍去),②以CE为对角线,连接PF交CE于G,CG=GE,PG=FG,得到G(0,﹣ ![]() ),设P(m,
),设P(m, ![]() m2﹣
m2﹣ ![]() m﹣2),则F(﹣m,
m﹣2),则F(﹣m, ![]() m﹣
m﹣ ![]() ),列方程得到此方程无实数根,于是得到结论.
),列方程得到此方程无实数根,于是得到结论.
【考点精析】解答此题的关键在于理解求根公式的相关知识,掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强学生课外阅读,开阔视野,某校开展了“书香校园,从我做起”的主题活动,学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频数分布表和频数分布直方图的一部分如下:
课外阅读时间(单位:小时)
频数(人数)
频率
0<t≤2
2
0.04
2<t≤4
3
0.06
4<t≤6
15
0.30
6<t≤8
a
0.50
t>8
5
b

请根据图表信息回答下列问题:
(1)频数分布表中的a= , b=;
(2)将频数分布直方图补充完整;
(3)学校将每周课外阅读时间在8小时以上的学生评为“阅读之星”,请你估计该校2000名学生中评为“阅读之星”的有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】某太阳能热水器的横截面示意图如图所示,已知真空热水管AB与支架CD所在直线相交于点O,且OB=OD,支架CD与水平线AE垂直,∠BAC=∠CDE=30°,DE=80cm,AC=165cm.

(1)求支架CD的长;
(2)求真空热水管AB的长.(结果保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:已知∠EDF的顶点D在△ABC的边AB所在直线上(不与A,B重合),DE交AC所在直线于点M,DF交BC所在直线于点N,记△ADM的面积为S1 , △BND的面积为S2 .
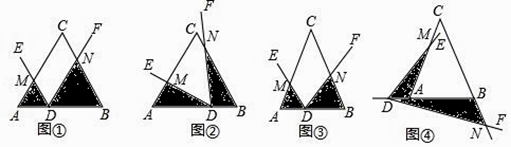
(1)初步尝试:如图①,当△ABC是等边三角形,AB=6,∠EDF=∠A,且DE∥BC,AD=2时,则S1S2=;
(2)类比探究:在(1)的条件下,先将点D沿AB平移,使AD=4,再将∠EDF绕点D旋转至如图②所示位置,求S1S2的值;
(3)延伸拓展:当△ABC是等腰三角形时,设∠B=∠A=∠EDF=α.
(Ⅰ)如图③,当点D在线段AB上运动时,设AD=a,BD=b,求S1S2的表达式(结果用a,b和α的三角函数表示).
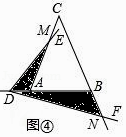
(Ⅱ)如图④,当点D在BA的延长线上运动时,设AD=a,BD=b,直接写出S1S2的表达式,不必写出解答过程.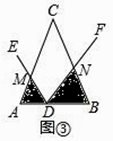
-
科目: 来源: 题型:
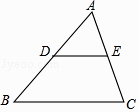
查看答案和解析>>【题目】如图,在△ABC中,D、E分别是边AB、AC的中点,则△ADE与△ABC的面积比S△ADE:S△ABC= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣2,1,3这三个数中任取两个不同的数,作为点的坐标.
(1)写出该点所有可能的坐标;
(2)求该点在第一象限的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
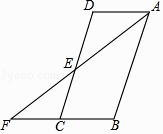
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°.求∠B的度数.
相关试题

