搜索
【题目】如图，在△ABC中，D、E分别是边AB、AC的中点，则△ADE与△ABC的面积比S△ADE：S△ABC= ．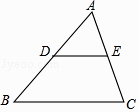 
参考答案：
【答案】1：4
【解析】解：∵D、E分别是边AB、AC的中点， ∴DE∥BC，DE= 
BC，
∴△ADE∽△ABC，
∴S△ADE：S△ABC=（ 
）2= 
，
所以答案是：1：4．
【考点精析】利用三角形中位线定理和相似三角形的判定与性质对题目进行判断即可得到答案，需要熟知连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某太阳能热水器的横截面示意图如图所示，已知真空热水管AB与支架CD所在直线相交于点O，且OB=OD，支架CD与水平线AE垂直，∠BAC=∠CDE=30°，DE=80cm，AC=165cm．
（1）求支架CD的长；
（2）求真空热水管AB的长．（结果保留根号） -
科目： 来源： 题型：
查看答案和解析>>【题目】问题背景：已知∠EDF的顶点D在△ABC的边AB所在直线上（不与A，B重合），DE交AC所在直线于点M，DF交BC所在直线于点N，记△ADM的面积为S1 ， △BND的面积为S2 ．
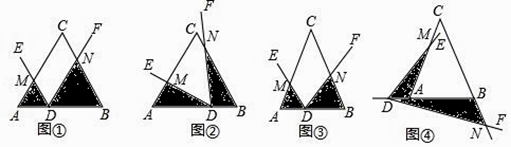
（1）初步尝试：如图①，当△ABC是等边三角形，AB=6，∠EDF=∠A，且DE∥BC，AD=2时，则S1S2=；
（2）类比探究：在（1）的条件下，先将点D沿AB平移，使AD=4，再将∠EDF绕点D旋转至如图②所示位置，求S1S2的值；
（3）延伸拓展：当△ABC是等腰三角形时，设∠B=∠A=∠EDF=α．
（Ⅰ）如图③，当点D在线段AB上运动时，设AD=a，BD=b，求S1S2的表达式（结果用a，b和α的三角函数表示）．
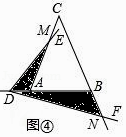
（Ⅱ）如图④，当点D在BA的延长线上运动时，设AD=a，BD=b，直接写出S1S2的表达式，不必写出解答过程．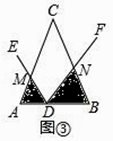
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=
x2+bx+c经过点B（3，0），C（0，﹣2），直线l：y=﹣ x﹣ 交y轴于点E，且与抛物线交于A，D两点，P为抛物线上一动点（不与A，D重合）．
（1）求抛物线的解析式；
（2）当点P在直线l下方时，过点P作PM∥x轴交l于点M，PN∥y轴交l于点N，求PM+PN的最大值．
（3）设F为直线l上的点，以E，C，P，F为顶点的四边形能否构成平行四边形？若能，求出点F的坐标；若不能，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】从﹣2，1，3这三个数中任取两个不同的数，作为点的坐标．
（1）写出该点所有可能的坐标；
（2）求该点在第一象限的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在ABCD中，DE=CE，连接AE并延长交BC的延长线于点F．
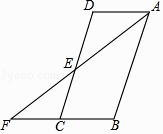
（1）求证：△ADE≌△FCE；
（2）若AB=2BC，∠F=36°．求∠B的度数．
相关试题
