【题目】如图,在ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.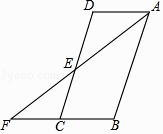
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°.求∠B的度数.
参考答案:
【答案】
(1)
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠D=∠ECF,
在△ADE和△FCE中,  ,
,
∴△ADE≌△FCE(ASA)
(2)
解:∵△ADE≌△FCE,
∴AD=FC,
∵AD=BC,AB=2BC,
∴AB=FB,
∴∠BAF=∠F=36°,
∴∠B=180°﹣2×36°=108°
【解析】(1)利用平行四边形的性质得出AD∥BC,AD=BC,证出∠D=∠ECF,由ASA即可证出△ADE≌△FCE;(2)证出AB=FB,由等腰三角形的性质和三角形内角和定理即可得出答案.
【考点精析】本题主要考查了平行四边形的性质的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2+bx+c经过点B(3,0),C(0,﹣2),直线l:y=﹣
x2+bx+c经过点B(3,0),C(0,﹣2),直线l:y=﹣  x﹣
x﹣  交y轴于点E,且与抛物线交于A,D两点,P为抛物线上一动点(不与A,D重合).
交y轴于点E,且与抛物线交于A,D两点,P为抛物线上一动点(不与A,D重合).
(1)求抛物线的解析式;
(2)当点P在直线l下方时,过点P作PM∥x轴交l于点M,PN∥y轴交l于点N,求PM+PN的最大值.
(3)设F为直线l上的点,以E,C,P,F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由. -
科目: 来源: 题型:
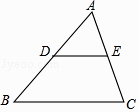
查看答案和解析>>【题目】如图,在△ABC中,D、E分别是边AB、AC的中点,则△ADE与△ABC的面积比S△ADE:S△ABC= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣2,1,3这三个数中任取两个不同的数,作为点的坐标.
(1)写出该点所有可能的坐标;
(2)求该点在第一象限的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某游乐场部分平面图如图所示,C、E、A在同一直线上,D、E、B在同一直线上,测得A处与E处的距离为80 米,C处与D处的距离为34米,∠C=90°,∠BAE=30°.(
 ≈1.4,
≈1.4,  ≈1.7)
≈1.7) 
(1)求旋转木马E处到出口B处的距离;
(2)求海洋球D处到出口B处的距离(结果保留整数). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线的解析式为y=﹣
 x2+bx+5.
x2+bx+5.
(1)当自变量 x≥2时,函数值y 随 x的增大而减少,求b 的取值范围;
(2)如图,若抛物线的图象经过点A(2,5),与x 轴交于点C,抛物线的对称轴与x 轴交于B.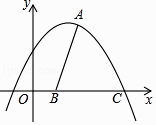
①求抛物线的解析式;
②在抛物线上是否存在点P,使得∠PAB=∠ABC?若存在,求出点P 的坐标;若不存在,请说明理由.
相关试题

