【题目】如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD.
(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20).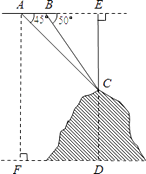
参考答案:
【答案】解:设EC=x,
在Rt△BCE中,tan∠EBC= ![]() ,
,
则BE= ![]() =
= ![]() x,
x,
在Rt△ACE中,tan∠EAC= ![]() ,
,
则AE= ![]() =x,
=x,
∵AB+BE=AE,
∴300+ ![]() x=x,
x=x,
解得:x=1800,
这座山的高度CD=DE﹣EC=3700﹣1800=1900(米).
答:这座山的高度是1900米
【解析】设EC=x,则在RT△BCE中,可表示出BE,在Rt△ACE中,可表示出AE,继而根据AB+BE=AE,可得出方程,解出即可得出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E.

(1)求证:△ABD≌△CAE;
(2)连接DE,线段DE与AB之间有怎样的位置和数量关系?请证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
 为
为 的角平分线上的一点,点
的角平分线上的一点,点 在边
在边 上.爱动脑筋的小刚经过仔细观察后,进行如下操作:在边
上.爱动脑筋的小刚经过仔细观察后,进行如下操作:在边 上取一点
上取一点 ,使得
,使得 ,这时他发现
,这时他发现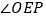 与
与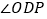 之间有一定的数量关系,请你写出
之间有一定的数量关系,请你写出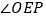 与
与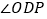 的数量关系__________.
的数量关系__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)3x﹣7+4x=6x﹣2
(2)4﹣3(2﹣x)=5x
(3)2(x+3)﹣5(1﹣x)=3(x﹣1)
(4)
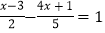 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,∠D=60°且AB=6,过O点作OE⊥AC,垂足为E.

(1)求OE的长;
(2)若OE的延长线交⊙O于点F,求弦AF、AC和弧CF围成的图形(阴影部分)的面积S. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:(A组:x<155; B组:155≤x<160; C组:160≤x<165; D组165≤x<170;E组:x≥170)
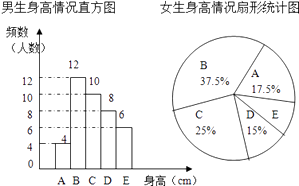
根据图表提供的信息,回答下列问题:
(1)样本中,男生的身高众数在组,中位数在组.
(2)样本中,女生的身高在E组的人数有人.
(3)已知该校共有男生400人,女生380人,请估计身高在160≤x<170之间的学生约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:小华遇到这样一个问题:
已知:如图1,在△ABC中,三边的长分别为AB= ,AC=
,AC=  ,BC=2,求∠A的正切值.
,BC=2,求∠A的正切值.
小华是这样解决问题的:
如图2所示,先在一个正方形网格(每个小正方形的边长均为1)中画出格点△ABC(△ABC三个顶点都在小正方形的顶点处),然后在这个正方形网格中再画一个和△ABC相似的格点△DEF,从而使问题得解.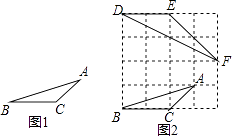
(1)如图2,△DEF中与∠A相等的角为 , ∠A的正切值为 .
(2)参考小华的方法请解决问题:若△LMN的三边分别为LM=2,MN=2 ,LN=2
,LN=2  ,求∠N的正切值.
,求∠N的正切值.
相关试题

