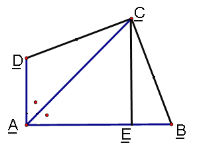
【题目】已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE
参考答案:
【答案】详见解析
【解析】
过点C作CF⊥AD交AD的延长线于F,根据角平分线上的点到角的两边距离相等可得CE=CF,根据同角的补角相等求出∠CDF=∠B,然后利用“角角边”证明△CDF和△CBE全等,根据全等三角形对应边相等可得DF=BE,再利用“HL”证明Rt△ACF和Rt△ACE全等,根据全等三角形对应边相等可得AE=AF,然后根据AF=AD+DF等量代换即可得证.
证明:如图,过点C作CF⊥AD交AD的延长线于F,
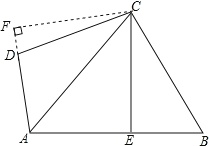
∵AC平分∠BAD,CE⊥AB,
∴CE=CF,
∵∠B+∠ADC=180°.
∠ADC+∠CDF=180°(平角定义),
∴∠CDF=∠B,
在△CDF和△CBE中,
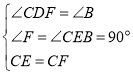 ,
,
∴△CDF≌△CBE(AAS),
∴DF=BE,
在Rt△ACF和Rt△ACE中,
![]() ,
,
∴Rt△ACF≌Rt△ACE(HL),
∴AE=AF,
∵AF=AD+DF,
∴AE=AD+BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)先化简,再求值:
 ,其中
,其中
(2)已知
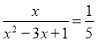 , 求
, 求 的值.
的值.(3)解方程
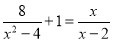
(4)当m为何值时,关于x的方程
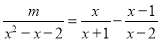 的解是正数.
的解是正数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一辆汽车在直线形的公路上由A向B行驶,M,N分别是位于AB两侧的村庄.

(1)设汽车行驶到公路AB上点P的位置时,距离村庄M最近,行驶到点Q的位置时,距离村庄N最近,在图中的公路AB上分别画出点P,Q位置.
(2)在公路AB上是否存在这样一点H,使汽车行驶到该点时,与村庄M,N的距离相等?如果存在请在图中AB上画出这一点,如果不存在请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)为了贯彻落实市委市府提出的“精准扶贫”精神.某校特制定了一系列关于帮扶A、B两贫困村的计划.现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如下表:

(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解:根据算术平方根的意义,由
 ,得(2x-y)2=9,所以2x-y=3.①(第一步)
,得(2x-y)2=9,所以2x-y=3.①(第一步)根据立方根的意义,由
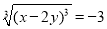 ,得x-2y=-3.②(第二步)
,得x-2y=-3.②(第二步)解得x=3,y=3.
把x、y的值代入分式中,得
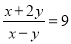 .(第三步)
.(第三步)上述解答有两处错误,一处是___________步,忽视了___________;另一处是步___________,忽视了___________.请写出正确的解答过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
 是等腰直角三角形,
是等腰直角三角形, ,AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点O,求证:
,AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点O,求证: .
.
-
科目: 来源: 题型:
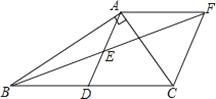
查看答案和解析>>【题目】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=3,AB=4,求菱形ADCF的面积.
相关试题

