【题目】如图所示,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点O,求证:
,AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点O,求证:![]() .
.

参考答案:
【答案】详见解析
【解析】
∠ADC和∠BDE所在的三角形肯定不全等,那么本题需要作辅助线.△ABC是等腰直角三角形,常用的辅助线是作三线里面的一线.可发现要证全等,已包含两个条件需利用全等得到另一边对应相等.
证明:如图: 作CH⊥AB于H交AD于P,
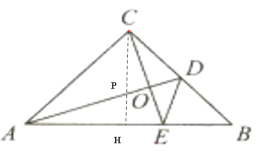
∵在Rt△ABC中,AC=CB,∠ACB=90°,
∴∠CAB=∠CBA=45°.
∴∠HCB=90°-∠CBA=45°=∠CBA=45°.
又∵BC中点为D,
∴CD=BD.
又CH⊥AB,
∴CH=AH=BH.
又∵∠PAH+∠APH=90°,∠PCO+∠CPO=90°,∠APH=∠CPO
∴∠PAH=∠ECH,
在△APH与△CEH中有:
∠PAH=∠ECH,AH=CH,∠PHA=∠EHC,
∴△APH≌△CEH(ASA).
∴PH=EH,
又PC=CH-PH,BE=BH-HE,
∴CP=EB.
∵△ACB是等腰直角三角形,
∴∠B=45°,即∠EBD=45°,CH⊥AB,
∴∠PCD=45°=∠EBD,
在△PDC与△EDB中有:
PC=EB,∠PCD=∠EBD,DC=DB,
∴△PDC≌△EDB(SAS).
∴∠ADC=∠EDB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)为了贯彻落实市委市府提出的“精准扶贫”精神.某校特制定了一系列关于帮扶A、B两贫困村的计划.现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如下表:

(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
-
科目: 来源: 题型:
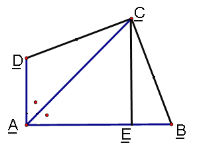
查看答案和解析>>【题目】已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE
-
科目: 来源: 题型:
查看答案和解析>>【题目】解:根据算术平方根的意义,由
 ,得(2x-y)2=9,所以2x-y=3.①(第一步)
,得(2x-y)2=9,所以2x-y=3.①(第一步)根据立方根的意义,由
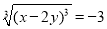 ,得x-2y=-3.②(第二步)
,得x-2y=-3.②(第二步)解得x=3,y=3.
把x、y的值代入分式中,得
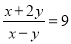 .(第三步)
.(第三步)上述解答有两处错误,一处是___________步,忽视了___________;另一处是步___________,忽视了___________.请写出正确的解答过程.
-
科目: 来源: 题型:
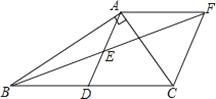
查看答案和解析>>【题目】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=3,AB=4,求菱形ADCF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一家小型放映厅盈利额y(元)与售票数x(张)之间的关系如图,保险部门规定:观众超过150人,要缴纳保险费50元,试根据图像回答问题:

(1)该放映厅有 个座位,该放映厅演出一场电影所需各项成本总和是 元;每张票的售价是 元;
(2)当售票数x为 时,不赔不赚:售票数x为 时,赔本;要获得最大利润150元,售票数x应为 张.
(3)当售票数x是多少张时,所得的利润和卖出150张时的利润相等(列方程解答)?当售票数满足什么条件时,此时利润比x=150张时多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=
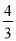 x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.
x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.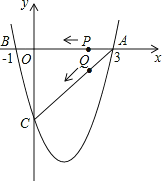
(1)求该二次函数的解析式及点C的坐标;
(2)当点P运动到B点时,点Q停止运动,这时,在x轴上是否存在点E,使得以A,E,Q为顶点的三角形为等腰三角形?若存在,请求出E点坐标;若不存在,请说明理由.
(3)当P,Q运动到t秒时,△APQ沿PQ翻折,点A恰好落在抛物线上D点处,请判定此时四边形APDQ的形状,并求出D点坐标.
相关试题

