【题目】(1)先化简,再求值: ![]() ,其中
,其中![]()
(2)已知![]() , 求
, 求![]() 的值.
的值.
(3)解方程![]()
(4)当m为何值时,关于x的方程![]() 的解是正数.
的解是正数.
参考答案:
【答案】(1)![]() ,1;(2)
,1;(2)![]() ;(3)原方程无解;(4)m<1且m≠-3.
;(3)原方程无解;(4)m<1且m≠-3.
【解析】
(1)先根据分式混合运算的法则把原式进行化简,再由![]() 得
得![]() 代入计算即可;
代入计算即可;
(2)先把条件和问题都变为相应的倒数,再利用分式的加法法则及完全平方公式计算即可;
(3)方程两边同乘以(x-2)(x+2),将分式方程转化为整式方程,解之求出x的值,再进一步检验即可得;
(4)根据解分式方程,可得分式方程的解,根据解为正数,可得不等式,根据解不等式,可得答案.
解:(1)原式![]()
![]()
![]()
![]()
∵![]()
∴![]()
∴原式=1;
(2)∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]() ;
;
(3)方程两边同乘(x-2)(x+2)得:8+(x-2)(x+2)=x(x+2),
解得x=2
检验:当x=2时,(x-2)(x+2)=0,
∴x=2是方程的增根,原方程无解.
(4)将方程两边都乘以(x2-x-2),得m=x(x-2)-(x-1)(x+1).
解这个方程,得![]() ,
,
∵原方程有增根时只能是x=-1或x=2.
当x=-1时,![]() =-1,解得m=3;
=-1,解得m=3;
当x=2时,![]() =2,解得m=-3.
=2,解得m=-3.
∴当m≠±3时,x=![]() 才是原方程的根.
才是原方程的根.
∵x>0,
∴![]() >0,
>0,
∴m<1.
∴m的取值范围是m<1且m≠-3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在边长为a的正方形中减去一个边长为b的小正方形(a>b),把剩下的部分拼成一个梯形如图,分别计算这两个图阴影部分的面积,验证了公式:_____用此公式计算:
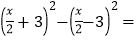 _____
_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD(如图①)按如下步骤操作:(1)以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E(如图②);(2)以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F(如图③);(3)将纸片展平,那么∠AFE的度数为_________.

-
科目: 来源: 题型:
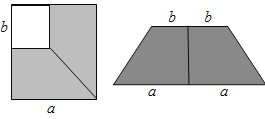
查看答案和解析>>【题目】如图,△ABC和△FPQ均是等边三角形,点D、E、F分别是△ABC三边的中点,点P在AB边上,连接EF、QE.若AB=6,PB=1,则QE= .
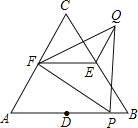
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一辆汽车在直线形的公路上由A向B行驶,M,N分别是位于AB两侧的村庄.

(1)设汽车行驶到公路AB上点P的位置时,距离村庄M最近,行驶到点Q的位置时,距离村庄N最近,在图中的公路AB上分别画出点P,Q位置.
(2)在公路AB上是否存在这样一点H,使汽车行驶到该点时,与村庄M,N的距离相等?如果存在请在图中AB上画出这一点,如果不存在请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)为了贯彻落实市委市府提出的“精准扶贫”精神.某校特制定了一系列关于帮扶A、B两贫困村的计划.现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如下表:

(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE
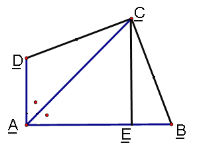
相关试题

