搜索
【题目】某天，某同学早上8点坐车从余姚图书馆出发去宁波大学，汽车离开余姚图书馆的距离
（千米）与所用时间
（分）之间的函数关系如图所示.已知汽车在途中停车加油一次，则下列描述不正确的是（ ）
A.汽车在途中加油用了10分钟
B.若
，则加满油以后的速度为80千米/小时
C.若汽车加油后的速度是90千米/小时，则
D.该同学
到达宁波大学
参考答案：
【答案】C
【解析】
根据图象逐一对选项进行分析即可.
A选项中,从图象可知AB段为停车加油，时间为10分钟，故该选项正确；
B选项中，若
，说明加油前后速度相同，全程60千米，除去加油的时间行驶了45分钟，速度为
，故该选项正确；
C选项中，若汽车加油后的速度是90千米/小时，则BC段行驶的路程为
，所以OA段的路程为60-30=30km，则
，故该选项错误；
D选项中，该同学8点出发，用了55分钟到达，故该选项正确.
故选C
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，函数
和
的图象分别为直线
，
，过点
作
轴的垂线交于点
，过点作
轴的垂线交于点
，过点作轴的垂线交于点
，过点作轴的垂线交于点
，…，依次进行下去，则点
的坐标为______，点
的坐标为______.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，直线l1：
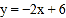与坐标轴交于A，B两点，直线l2：
（
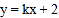≠0）与坐标轴交于点C，D.（1）求点A，B的坐标；
（2）如图，当
=2时，直线l1，l2与相交于点E，求两条直线与
轴围成的△BDE的面积；（3）若直线l1，l2与
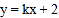轴不能围成三角形，点P（a，b）在直线l2：（k≠0）上，且点P在第一象限.①求
的值；②若
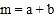,，求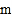
的取值范围.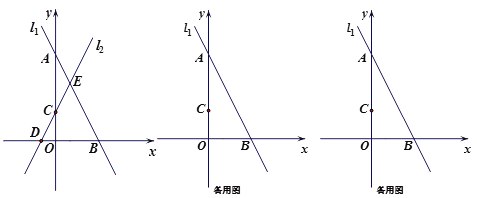
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两地相距300千米，一辆货车和一辆轿车分别从甲地开往乙地（轿车的平均速度大于货车的平均速度），如图，线段
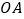、折线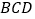
分别表示两车离甲地的距离
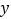（单位：千米）与时间
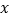（单位：小时）之间的函数关系.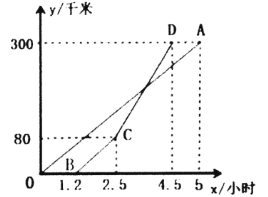
（1）线段
与折线中，______（填线段或折线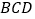）表示货车离甲地的距离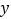与时间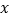之间的函数关系.（2）求线段
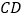的函数关系式（标出自变量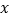取值范围）；（3）货车出发多长时间两车相遇？
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义：两边的平方和与这两边乘积的差等于第三边平方的三角形叫做“和谐三角形”.如图1在
中，若
，则是“和谐三角形”.
（1）等边三角形一定是“和谐三角形”，是______命题（填“真”或“假”）.
（2）若
中，
，
，
，
，且
，若是“和谐三角形”，求
.（3）如图2，在等边三角形
的边
，
上各取一点
，
，且
，
，
相交于点
，
是
的高，若
是“和谐三角形”，且
.
①求证：
.②连结
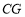，若
，那么线段
，
，
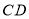能否组成一个“和谐三角形”？若能，请给出证明：若不能，请说明理由. -
科目： 来源： 题型：
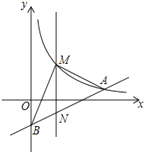
查看答案和解析>>【题目】如图，在平面直角坐标系中，已知点A（8，1），B（0，﹣3），反比例函数y=
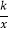（x＞0）的图象经过点A，动直线x=t（0＜t＜8）与反比例函数的图象交于点M，与直线AB交于点N．（1）k的值是______；
（2）当t=4时，求△BMN面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在
中，
是
的中点，
是边上一动点，连结
，取的中点
，连结
.小梦根据学习函数的经验，对
的面积与
的长度之间的关系进行了探究：
（1）设
的长度为
，的面积
，通过取边上的不同位置的点，经分析和计算，得到了与的几组值，如下表：0
1
2
3
4
5
6
3
1
0
2
3
根据上表可知，
______，
______.（2）在平面直角坐标系
中，画出（1）中所确定的函数的图象.
（3）在（1）的条件下，令
的面积为
.①用
的代数式表示.②结合函数图象.解决问题：当
时，的取值范围为______.
相关试题
