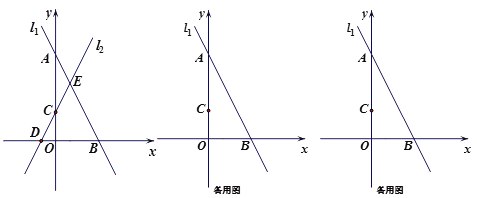
【题目】在平面直角坐标系中,直线l1:![]() 与坐标轴交于A,B两点,直线l2:
与坐标轴交于A,B两点,直线l2:![]() (
(![]() ≠0)与坐标轴交于点C,D.
≠0)与坐标轴交于点C,D.
(1)求点A,B的坐标;
(2)如图,当![]() =2时,直线l1,l2与相交于点E,求两条直线与
=2时,直线l1,l2与相交于点E,求两条直线与![]() 轴围成的△BDE的面积;
轴围成的△BDE的面积;
(3)若直线l1,l2与![]() 轴不能围成三角形,点P(a,b)在直线l2:
轴不能围成三角形,点P(a,b)在直线l2:![]() (k≠0)上,且点P在第一象限.
(k≠0)上,且点P在第一象限.
①求![]() 的值;
的值;
②若![]() ,,求
,,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)A(0,6)B(3,0)(2)8(3)①![]() ;②
;②![]()
【解析】
(1)根据![]() ,令x=0,得到y=6;令y=0,得到x=3,即可解答;
,令x=0,得到y=6;令y=0,得到x=3,即可解答;
(2)当![]() =2时,求出直线l2:
=2时,求出直线l2:![]() 与x轴交点D的坐标,从而求出DB的长,再把
与x轴交点D的坐标,从而求出DB的长,再把
两直线的解析式组成方程组求出点E的坐标,根据三角形的面积公式求出△BDE的面积;
(3)①若直线l1,l2与![]() 轴不能围成三角形,则直线l2与l1平行或直线l2经过点B,从而求出k的值;②根据k的值分别求出直线l2解析式,再根据点P (a,b)在直线l2 上得到a与b的关系式,从而确定
轴不能围成三角形,则直线l2与l1平行或直线l2经过点B,从而求出k的值;②根据k的值分别求出直线l2解析式,再根据点P (a,b)在直线l2 上得到a与b的关系式,从而确定![]() 的取值范围.
的取值范围.
(1)∵![]() ,
,
∴令x=0,得到y=6;令y=0,得到x=3,
则A(0,6),B(3,0);
(2)当![]() =2时,直线l2:
=2时,直线l2:![]()
令y=0,得到x=-1,
∴D(-1,0)
∴BD=4
由![]()
解得:![]()
∴点E坐标为(1,4)
∴![]() 4=8
4=8
(3)①若直线l1,l2与![]() 轴不能围成三角形,则直线l2与l1平行或直线l2经过点B,
轴不能围成三角形,则直线l2与l1平行或直线l2经过点B,
当直线l2与l1平行,k=-2,当直线l2经过点B时,![]() =0,则
=0,则![]() =-
=-![]()
∴k=-2或-![]()
②当k=-2时,直线l2的解析式为:![]() ,
,
∵点P(a,b)在直线l2上,∴b=-2a+2
∴![]() =a-2a+2=2-a
=a-2a+2=2-a
∵点P(a,b)在第一象限
∴![]()
解得:0![]()
∴1![]() 2-a
2-a![]() ,即1
,即1![]()
当k=-![]() 时,直线l2的解析式为:
时,直线l2的解析式为:![]() ,
,
∵点P(a,b)在直线l2上,∴b=![]() a+2
a+2
∴![]() =a-
=a-![]() a+2=
a+2=![]() a+2
a+2
∵点P(a,b)在第一象限
∴
解得:0![]()
∴2![]() a+2
a+2![]() ,即2
,即2![]()
综上所述:![]() 的取值范围为:1
的取值范围为:1![]() 或2
或2![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A城出发沿一条笔直公路匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离
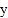 (千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.
(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.(1)A,B两城相距 千米,乙车比甲车早到 小时;
(2)甲车出发多长时间与乙车相遇?
(3)若两车相距不超过20千米时可以通过无线电相互通话,则两车都在行驶过程中可以通过无线电通话的时间有多长?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知长方形
 中,
中,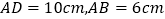 ,点
,点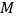 在边
在边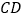 上,由
上,由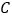 往
往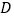 运动,速度为
运动,速度为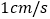 ,运动时间为
,运动时间为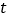 秒,将
秒,将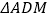 沿着
沿着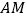 翻折至
翻折至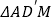 ,点
,点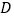 对应点为
对应点为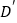 ,
,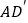 所在直线与边
所在直线与边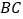 交与点
交与点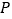 ,
,(1)如图
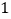 ,当
,当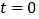 时,求证:
时,求证: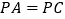 ;
;(2)如图
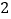 ,当
,当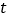 为何值时,点
为何值时,点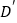 恰好落在边
恰好落在边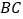 上;
上;(3)如图
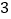 ,当
,当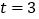 时,求
时,求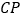 的长.
的长.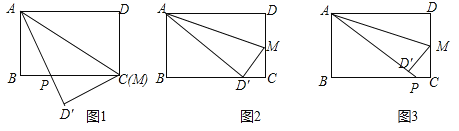
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的B′处,得到折痕EC,将点A落在直线EF上的点A′处,得到折痕EN.
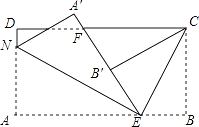
(1)若∠BEB′=110°,则∠BEC=°,∠AEN=°,∠BEC+∠AEN=°.
(2)若∠BEB′=m°,则(1)中∠BEC+∠AEN的值是否改变?请说明你的理由.
(3)将∠ECF对折,点E刚好落在F处,且折痕与B′C重合,求∠DNA′. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,BD是直径.若
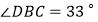 ,则
,则 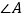 等于( )
等于( )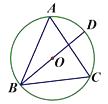
A.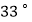

B.
C.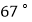
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD长( )

A.4 cm
cm
B.3 cm
cm
C.5 cm
cm
D.4 cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
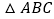 中,
中,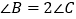 ,
,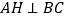 ,
,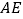 平分
平分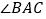 ,
,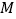 是
是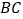 中点,则下列结论正确的个数为( )
中点,则下列结论正确的个数为( )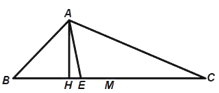
(1)
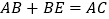 (2)
(2)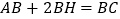 (3)
(3)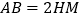 (4)
(4)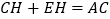
A. 1B. 2C. 3D. 4
相关试题

