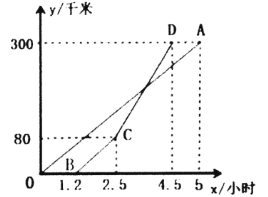
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车分别从甲地开往乙地(轿车的平均速度大于货车的平均速度),如图,线段![]() 、折线
、折线![]() 分别表示两车离甲地的距离
分别表示两车离甲地的距离![]() (单位:千米)与时间
(单位:千米)与时间![]() (单位:小时)之间的函数关系.
(单位:小时)之间的函数关系.
(1)线段![]() 与折线
与折线![]() 中,______(填线段
中,______(填线段![]() 或折线
或折线![]() )表示货车离甲地的距离
)表示货车离甲地的距离![]() 与时间
与时间![]() 之间的函数关系.
之间的函数关系.
(2)求线段![]() 的函数关系式(标出自变量
的函数关系式(标出自变量![]() 取值范围);
取值范围);
(3)货车出发多长时间两车相遇?
参考答案:
【答案】(1)OA;(2)y=110x195(2.5≤x≤4.5);(3)3.9小时.
【解析】
(1)根据题意可以分别求得两个图象中相应函数对应的速度,从而可以解答本题;
(2)设CD段的函数解析式为y=kx+b,将C(2.5,80),D(4.5,300)两点的坐标代入,运用待定系数法即可求解;
(3)根据题意可以求得OA对应的函数解析式,从而可以解答本题.
(1)线段OA表示货车货车离甲地的距离y与时间x之间的函数关系,
理由:vOA=![]() (千米/时),vBCD=
(千米/时),vBCD=![]()
∵60<![]() 90轿车的平均速度大于货车的平均速度,
90轿车的平均速度大于货车的平均速度,
∴线段OA表示货车离甲地的距离y与时间x之间的函数关系.
故答案为:OA;
(2)设CD段函数解析式为y=kx+b(k≠0)(2.5≤x≤4.5).
∵C(2.5,80),D(4.5,300)在其图象上,
∴![]()
解得![]()
∴CD段函数解析式:y=110x195(2.5≤x≤4.5);
(3)设线段OA对应的函数解析式为y=kx,
300=5k,得k=60,
即线段OA对应的函数解析式为y=60x,
![]() ,解得
,解得![]()
即货车出发3.9小时两车相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点
 、点
、点 表示的数分别为
表示的数分别为 、
、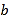 ,则
,则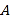 、
、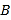 两点之间的距离
两点之间的距离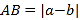 ,线段
,线段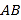 的中点表示的数为
的中点表示的数为 .
.(问题情境)
如图,数轴上点
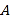 表示的数为
表示的数为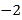 ,点
,点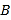 表示的数为8,点
表示的数为8,点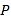 从点
从点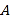 出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点
出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点 从点
从点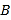 出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为
出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为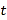 秒(
秒(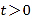 ).
).(综合运用)
(1)填空:
①
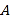 、
、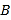 两点之间的距离
两点之间的距离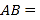 ________,线段
________,线段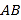 的中点表示的数为__________.
的中点表示的数为__________.②用含
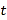 的代数式表示:
的代数式表示: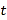 秒后,点
秒后,点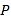 表示的数为____________;点
表示的数为____________;点 表示的数为___________.
表示的数为___________.③当
 _________时,
_________时,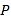 、
、 两点相遇,相遇点所表示的数为__________.
两点相遇,相遇点所表示的数为__________.(2)当
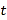 为何值时,
为何值时,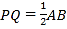 .
.(3)若点
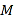 为
为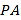 的中点,点
的中点,点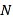 为
为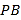 的中点,点
的中点,点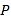 在运动过程中,线段
在运动过程中,线段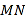 的长度是否发生变化?若变化,请说明理由;若不变,请求出线段
的长度是否发生变化?若变化,请说明理由;若不变,请求出线段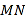 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,函数
 和
和 的图象分别为直线
的图象分别为直线 ,
, ,过点
,过点 作
作 轴的垂线交
轴的垂线交 于点
于点 ,过
,过 点作
点作 轴的垂线交
轴的垂线交 于点
于点 ,过点
,过点 作
作 轴的垂线交
轴的垂线交 于点
于点 ,过点
,过点 作
作 轴的垂线交
轴的垂线交 于点
于点 ,…,依次进行下去,则点
,…,依次进行下去,则点 的坐标为______,点
的坐标为______,点 的坐标为______.
的坐标为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,直线l1:
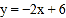 与坐标轴交于A,B两点,直线l2:
与坐标轴交于A,B两点,直线l2: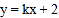 (
( ≠0)与坐标轴交于点C,D.
≠0)与坐标轴交于点C,D.(1)求点A,B的坐标;
(2)如图,当
 =2时,直线l1,l2与相交于点E,求两条直线与
=2时,直线l1,l2与相交于点E,求两条直线与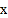 轴围成的△BDE的面积;
轴围成的△BDE的面积;(3)若直线l1,l2与
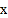 轴不能围成三角形,点P(a,b)在直线l2:
轴不能围成三角形,点P(a,b)在直线l2: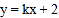 (k≠0)上,且点P在第一象限.
(k≠0)上,且点P在第一象限.①求
 的值;
的值;②若
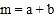 ,,求
,,求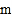 的取值范围.
的取值范围.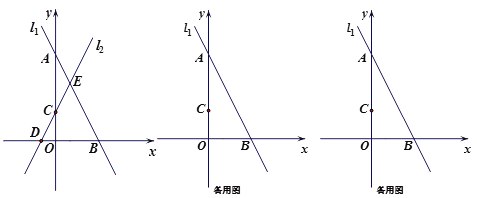
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天,某同学早上8点坐车从余姚图书馆出发去宁波大学,汽车离开余姚图书馆的距离
 (千米)与所用时间
(千米)与所用时间 (分)之间的函数关系如图所示.已知汽车在途中停车加油一次,则下列描述不正确的是( )
(分)之间的函数关系如图所示.已知汽车在途中停车加油一次,则下列描述不正确的是( )
A.汽车在途中加油用了10分钟
B.若
 ,则加满油以后的速度为80千米/小时
,则加满油以后的速度为80千米/小时C.若汽车加油后的速度是90千米/小时,则

D.该同学
 到达宁波大学
到达宁波大学 -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:两边的平方和与这两边乘积的差等于第三边平方的三角形叫做“和谐三角形”.如图1在
 中,若
中,若 ,则
,则 是“和谐三角形”.
是“和谐三角形”.
(1)等边三角形一定是“和谐三角形”,是______命题(填“真”或“假”).
(2)若
 中,
中, ,
, ,
, ,
, ,且
,且 ,若
,若 是“和谐三角形”,求
是“和谐三角形”,求 .
.(3)如图2,在等边三角形
 的边
的边 ,
, 上各取一点
上各取一点 ,
, ,且
,且 ,
, ,
, 相交于点
相交于点 ,
, 是
是 的高,若
的高,若 是“和谐三角形”,且
是“和谐三角形”,且 .
.
①求证:
 .
.②连结
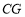 ,若
,若 ,那么线段
,那么线段 ,
, ,
, 能否组成一个“和谐三角形”?若能,请给出证明:若不能,请说明理由.
能否组成一个“和谐三角形”?若能,请给出证明:若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(8,1),B(0,﹣3),反比例函数y=
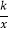 (x>0)的图象经过点A,动直线x=t(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.
(x>0)的图象经过点A,动直线x=t(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.(1)k的值是______;
(2)当t=4时,求△BMN面积.
相关试题

