【题目】某校开展了以“人生观、价值观”为主题的班队活动.活动结束后,初三(2)班数学兴趣小组提出了5个主要观点并在本班50名学生中进行了调査(要求每位同学只选自己最认可的一项观点),并制成了如图所示的扇形统计图. 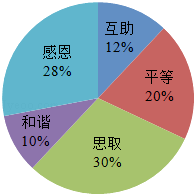
(1)该班学生选择“和谐”观点的有人,在扇形统计图中,“和谐”观点所在扇形区域的圆心角是 .
(2)如果该校有1500名初三学生.利用样本估计选择“感恩”观点的初三学生约有人.
(3)如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查.求恰好选到“和谐”和“感恩”观点的概率.
参考答案:
【答案】
(1)5;36°
(2)420
(3)解:
互动 | 平等 | 思取 | 和谐 | 感恩 | |
互动 | (互动,平等) | (互动,思取) | (互动,和谐) | (互动,感恩) | |
平等 | (平等,互动) | (平等,思取) | (平等,和谐) | (平等,感恩) | |
思取 | (思取,互动) | (思取,平等) | (思取,和谐) | (思取,感恩) | |
和谐 | (和谐,互动) | (和谐,平等) | (和谐,思取) | (和谐,感恩) | |
感恩 | (感恩,互动) | (感恩,平等) | (感恩,思取) | (感恩,和谐) |
∴恰好选到“和谐”和“感恩”观点的概率= ![]()
【解析】解:(1)共调查了50名学生,选择“和谐”观点的占10%, 50×10%=5,360°×10%=36°;(2)∵选择“感恩”的占28%,
∴1500×28%=420人,
【考点精析】根据题目的已知条件,利用扇形统计图和列表法与树状图法的相关知识可以得到问题的答案,需要掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(﹣2,﹣3),若B是x轴上一动点,则A、B两点的距离的最小值为( )
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)计算:3( ﹣π)0﹣
﹣π)0﹣  +(﹣1)2011
+(﹣1)2011
(2)先化简,再求值: ,其中x=
,其中x=  -3.
-3.
(3)如图,平行四边形ABCD的对角线AC、BD交于点O,E、F在AC上,G、H在BD上,且AF=CE,BH=DG. 求证:GF∥HE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品50件.生产一件A产品需要甲种原料9千克,乙种原料3千克,可获利润700元;生产一件B产品,需要甲种原料4千克,乙种原料10千克,可获利润1200元.
(1)设生产x件A种产品,写出其题意x应满足的不等式组;
(2)由题意有哪几种按要求安排A、B两种产品的生产件数的生产方案?请您帮助设计出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句中,命题有_______个.
①对顶角相等;②内错角相等;③∠1>∠2吗?④若a∥b,b∥c,则a∥c;⑤两点确定一条直线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了直观地表示我国体育健儿在最近八届夏季奥运会上获得奖牌总数的变化趋势,最适合使用的统计图是( )
A.扇形图B.折线图C.条形图D.直方图
-
科目: 来源: 题型:
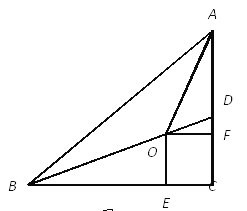
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90,BD是△ABC的角平分线,点O在BD上,分别过点O作OE⊥BC,OF⊥AC,垂足为E,F,且OE=OF.
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
相关试题

