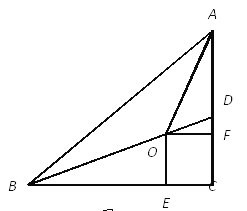
【题目】如图,在Rt△ABC中,∠C=90,BD是△ABC的角平分线,点O在BD上,分别过点O作OE⊥BC,OF⊥AC,垂足为E,F,且OE=OF.
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
参考答案:
【答案】(1)证明见解析;(2)OE=2.
【解析】试题分析:(1)过点O作OM⊥AB,由角平分线的性质得OE=OM,由正方形的性质得OE=OF,易得OM=OF,由角平分线的判定定理得点O在∠BAC的平分线上;
(2)连接OC,根利用勾股定理求出AB的长,据三角形的面积公式即可得出结论.
试题解析:(1)证明:过点O作OM⊥AB于点M.
因为BD平分∠ABC,OM⊥AB于M,OE⊥BC于E,所以OM=OE.
又OE=OF,所以OM=OF.所以点O在∠BAC的平分线上.
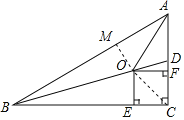
(2)连接OC.在Rt△ABC中,∠C=90°,AC=5,BC=12,根据勾股定理,得AB=13.
因为S△ABO+S△BCO+S△ACO =S△ABC,所以![]() ×13·OM+
×13·OM+![]() ×12·OE+
×12·OE+![]() ×5·OF=
×5·OF=![]() ×5×12.
×5×12.
由(1)知OM=OE=OF,所以15OE=30,解得OE=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开展了以“人生观、价值观”为主题的班队活动.活动结束后,初三(2)班数学兴趣小组提出了5个主要观点并在本班50名学生中进行了调査(要求每位同学只选自己最认可的一项观点),并制成了如图所示的扇形统计图.
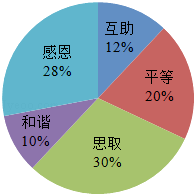
(1)该班学生选择“和谐”观点的有人,在扇形统计图中,“和谐”观点所在扇形区域的圆心角是 .
(2)如果该校有1500名初三学生.利用样本估计选择“感恩”观点的初三学生约有人.
(3)如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查.求恰好选到“和谐”和“感恩”观点的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句中,命题有_______个.
①对顶角相等;②内错角相等;③∠1>∠2吗?④若a∥b,b∥c,则a∥c;⑤两点确定一条直线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了直观地表示我国体育健儿在最近八届夏季奥运会上获得奖牌总数的变化趋势,最适合使用的统计图是( )
A.扇形图B.折线图C.条形图D.直方图
-
科目: 来源: 题型:
查看答案和解析>>【题目】按照题中提供的思路点拨,先填空,然后完成解答的全过程.
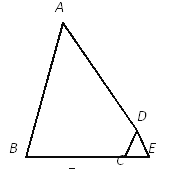
如图,已知AB=AD,∠BAD=60°,∠BCD=120°,延长BC,使CE=CD,连接DE,求证:BC+DC=AC.
思路点拨:(1)由已知条件AB=AD,∠BAD=60°,可知△ABD是_三角形.同理由已知条件∠BCD=120°得到∠DCE=_,且CE=CD,可知_;
(2)要证BC+DC=AC,可将问题转化为证两条线段相等,即_=_;
(3)要证(2)中所填写的两条线段相等,可以先证明_.请写出完整的证明过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为保护环境,我市公交公司计划购买A型和B型两种环保节能公交车共10辆.若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?
(3)在(2)的条件下,哪种购车方案总费用最少?最少总费用是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程3x+1=m+4的解是x=2,则m值是( )
A.2B.5C.3D.1
相关试题

