【题目】如图,以△ABC的一边AB为直径作⊙O,交AC,BC于D,E两点,若AB=4,∠BED=120°,点E是BD中点,则图中阴影部分的面积是( )

A. 4 B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】D
【解析】连接OE、OD、AE.
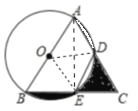
∵∠BED=120°,
∴∠BAC=60°,
∵![]() ,
,
∴BE=ED,
∵OB=OE=OD,
∴△OEB≌△OED,
∴∠OEB=∠OED=60°,
∴∠ABC=∠BAC=60°,
∴△ABC是等边三角形,
∴AB=BC=AC=4,
∵AB为直径,
∴∠AEB=90°,BE=EC=![]() BC=2,
BC=2,
∵OB=OE,∠ABC=∠BAC=60°,OA=OD,
∴△OBE、△AOD、△ODE、△CDE都是等边三角形,
∴OB=BE=OE=2,OA=OD=AD=2,∠AOD=∠BOE=60°,
∴∠EOD=180°﹣60°﹣60°=60°,
∴阴影部分的面积是=(扇形BOE的面积﹣三角形BOE面积)+(菱形OECD的面积﹣扇形OED的面积)=三角形CDE的面积=![]() ×22=
×22=![]() .
.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,三角形
 的三个顶点的位置如图,
的三个顶点的位置如图, 为三角形
为三角形 内一点,
内一点, 的坐标为
的坐标为
(1)平移三角形
 ,使
,使 点与原点重合,请画出平移后的三角形
点与原点重合,请画出平移后的三角形
(2)直接写出
 的对应点
的对应点 的坐标;并写出平移的规律.
的坐标;并写出平移的规律. ( , );
( , ); ( , );
( , ); ( , );
( , );(3)求三角形
 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划生产
 两种产品共10件,其生产成本和销售价如下表所示:
两种产品共10件,其生产成本和销售价如下表所示:产品
 种产品
种产品 种产品
种产品成本(万元/件)
3
5
售价(万元/件)
4
7
(1)若工厂计划获利14万元,则应分别生产
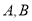 两种产品多少件?
两种产品多少件?(2)若工厂投入资金不多于44万元,且获利不少于14万元,则工厂有哪些生产方案?
(3)在第(2)的条件下,哪种方案获利最大;最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,四边形
 为长方形,其中点
为长方形,其中点 的坐标分别为
的坐标分别为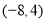 、
、 ,且
,且 轴,交
轴,交 轴于点
轴于点 ,
, 交
交 轴于点
轴于点 .
.(1)求
 两点坐标;
两点坐标;(2)一动点
 从
从 出发,以2个单位/秒的速度沿
出发,以2个单位/秒的速度沿 向
向 点运动(不与
点运动(不与 点重合),在
点重合),在 点运动过程中,连接
点运动过程中,连接 ,
,①试探究
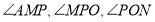 之间的数量关系;并说明理由;
之间的数量关系;并说明理由;②是否存在某一时刻
 ,使三角形
,使三角形 的面积等于长方形
的面积等于长方形 面积的
面积的 ?若存在,求
?若存在,求 的值并求此时点
的值并求此时点 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;③三角形
 的面积记作
的面积记作 ;三角形
;三角形 的面积记作
的面积记作 ;三角形
;三角形 的面积记作
的面积记作 ;直接写出
;直接写出 、
、 、
、 的关系.
的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】五一小长假的某一天,亮亮全家上午
 时自驾小汽车从家里出发,到某旅游景点游玩,该小汽车离家的距离(千米)与时间(时)之间的关系如图所示,根据图像提供的有关信息,判断下列说法错误的是( )
时自驾小汽车从家里出发,到某旅游景点游玩,该小汽车离家的距离(千米)与时间(时)之间的关系如图所示,根据图像提供的有关信息,判断下列说法错误的是( )
A.景点离亮亮的家
 千米
千米B.亮亮到家的时间为
 时
时C.小汽车返程的速度为
 千米/时
千米/时D.
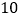 时至
时至 时,小汽车匀速行驶
时,小汽车匀速行驶 -
科目: 来源: 题型:
查看答案和解析>>【题目】小芳和小刚都想参加学校组织的暑期实践活动,但只有一个名额,小芳提议:将一个转盘
 等分,分别将
等分,分别将 个区间标上
个区间标上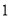 至个
至个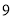 号码,随意转动一次转盘,根据指针指向区间决定谁去参加活动,具体规则:若指针指向偶数区间,小刚去参加活动;若指针指向奇数区间,小芳去参加活动.
号码,随意转动一次转盘,根据指针指向区间决定谁去参加活动,具体规则:若指针指向偶数区间,小刚去参加活动;若指针指向奇数区间,小芳去参加活动.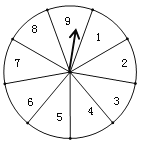
(1)求小刚去参加活动的概率是多少?(2)你认为这个游戏公平吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

相关试题

