【题目】在平面直角坐标系中,三角形![]() 的三个顶点的位置如图,
的三个顶点的位置如图,![]() 为三角形
为三角形![]() 内一点,
内一点,![]() 的坐标为
的坐标为![]()
(1)平移三角形![]() ,使
,使![]() 点与原点重合,请画出平移后的三角形
点与原点重合,请画出平移后的三角形![]()
(2)直接写出![]() 的对应点
的对应点![]() 的坐标;并写出平移的规律.
的坐标;并写出平移的规律.
![]() ( , );
( , );
![]() ( , );
( , );
![]() ( , );
( , );
(3)求三角形![]() 的面积.
的面积.
参考答案:
【答案】(1)画![]() 见解析;(2)
见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)点C平移到原点,即点C向左平移1个单位,向下平移两个单位,按同样的方法平移点A、B即可;
(2)由图中坐标系即可写出平移后点的坐标,易得平移规律;
(3)用A、B、C三点所在的长方形的面积减去三个直角三角形的面积即可.
(1)![]() 如图所示:
如图所示:

(2)∵点![]() 的对应点
的对应点![]() 的坐标为
的坐标为![]() ,∴平移规律是:先向左平移1个单位长度,再向下平移2个单位长度,
,∴平移规律是:先向左平移1个单位长度,再向下平移2个单位长度,
∴![]()
(3)如图所示

所以三角形![]() 的面积为
的面积为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的二次函数y=x2-(2m-1)x+m2+3m+4.
(1)探究m取不同值时,二次函数y的图象与x轴的交点的个数情况;
(2)设二次函数的图象与x轴的交点为A(x1,0),B(x2,0),且x12+x22=5,与y轴的交点为C,它的顶点为M,求直线CM的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,美丽的弦图,蕴含着四个全等的直角三角形.已知每个直角三角形较长的直角边为a,较短的直角边为b,斜边长为c.如图②,现将这四个全图②等的直角三角形紧密拼接,形成飞镖状,已知外围轮廓(实线)的周长为24,OC=3,则该飞镖状图案的面积( )
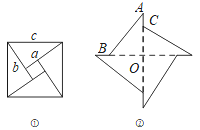
A. 6 B. 12 C. 24 D. 24
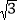
-
科目: 来源: 题型:
查看答案和解析>>【题目】使得函数值为零的自变量的值称为函数的零点.例如,对于函数y=x-1,令y=0可得x=1,我们就说1是函数y=x-1的零点.
已知y=x2-2mx-2(m+3)(m为常数).
(1)当m=0时,求该函数的零点;
(2)证明:无论m取何值,该函数总有两个零点;
(3)设函数的两个零点分别为x1和x2,且
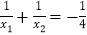 ,此时函数图象与x轴的交点分别为A,B(点A在点B左侧),点M在直线y=x-10上,当MA+MB最小时,求直线AM的函数表达式.
,此时函数图象与x轴的交点分别为A,B(点A在点B左侧),点M在直线y=x-10上,当MA+MB最小时,求直线AM的函数表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划生产
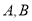 两种产品共10件,其生产成本和销售价如下表所示:
两种产品共10件,其生产成本和销售价如下表所示:产品
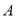 种产品
种产品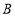 种产品
种产品成本(万元/件)
3
5
售价(万元/件)
4
7
(1)若工厂计划获利14万元,则应分别生产
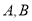 两种产品多少件?
两种产品多少件?(2)若工厂投入资金不多于44万元,且获利不少于14万元,则工厂有哪些生产方案?
(3)在第(2)的条件下,哪种方案获利最大;最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,四边形
 为长方形,其中点
为长方形,其中点 的坐标分别为
的坐标分别为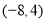 、
、 ,且
,且 轴,交
轴,交 轴于点
轴于点 ,
, 交
交 轴于点
轴于点 .
.(1)求
 两点坐标;
两点坐标;(2)一动点
 从
从 出发,以2个单位/秒的速度沿
出发,以2个单位/秒的速度沿 向
向 点运动(不与
点运动(不与 点重合),在
点重合),在 点运动过程中,连接
点运动过程中,连接 ,
,①试探究
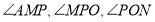 之间的数量关系;并说明理由;
之间的数量关系;并说明理由;②是否存在某一时刻
 ,使三角形
,使三角形 的面积等于长方形
的面积等于长方形 面积的
面积的 ?若存在,求
?若存在,求 的值并求此时点
的值并求此时点 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;③三角形
 的面积记作
的面积记作 ;三角形
;三角形 的面积记作
的面积记作 ;三角形
;三角形 的面积记作
的面积记作 ;直接写出
;直接写出 、
、 、
、 的关系.
的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以△ABC的一边AB为直径作⊙O,交AC,BC于D,E两点,若AB=4,∠BED=120°,点E是BD中点,则图中阴影部分的面积是( )

A. 4 B.
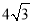 C.
C. 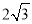 D.
D. 
相关试题

