【题目】某工厂计划生产![]() 两种产品共10件,其生产成本和销售价如下表所示:
两种产品共10件,其生产成本和销售价如下表所示:
产品 |
|
|
成本(万元/件) | 3 | 5 |
售价(万元/件) | 4 | 7 |
(1)若工厂计划获利14万元,则应分别生产![]() 两种产品多少件?
两种产品多少件?
(2)若工厂投入资金不多于44万元,且获利不少于14万元,则工厂有哪些生产方案?
(3)在第(2)的条件下,哪种方案获利最大;最大利润是多少?
参考答案:
【答案】(1)生产![]() 种产品6件,生产
种产品6件,生产![]() 种产品4件;
种产品4件;
(2)工厂共有4种生产方案:方案一:![]() 种产品生产3件,
种产品生产3件,![]() 种产品生产7件;方案二:
种产品生产7件;方案二:![]() 种产品生产4件,
种产品生产4件,![]() 种产品生产6件;方案三:
种产品生产6件;方案三:![]() 种产品生产5件,
种产品生产5件,![]() 种产品生产5件;方案四:
种产品生产5件;方案四:![]() 种产品生产6件,
种产品生产6件,![]() 种产品生产4件;(3)方案一获利最大为17万元.
种产品生产4件;(3)方案一获利最大为17万元.
【解析】
(1)可设生产![]() 种
种![]() 件,则生产
件,则生产![]() 种
种![]() 件,求出
件,求出![]() 种产品、
种产品、![]() 种产品每件获利的钱数,列出关于x的方程求解即可;
种产品每件获利的钱数,列出关于x的方程求解即可;
(2)可设![]() 种产品
种产品![]() 件,
件,![]() 种产品
种产品![]() 件,根据题意列出关于m的不等式组,求出m的取值范围可得生产方案;
件,根据题意列出关于m的不等式组,求出m的取值范围可得生产方案;
(3)由(1)可知所获利润y与生产A种产品的件数x间的关系式,据此即可判断获利最大的方案.
(1)设生产![]() 种
种![]() 件,生产
件,生产![]() 种
种![]() 件
件
∵![]() 种产品成本3万元/件,售价4万元/件,
种产品成本3万元/件,售价4万元/件,
∴![]() 种产品获利1万元/件,同理可得
种产品获利1万元/件,同理可得![]() 种产品获利2万元/件
种产品获利2万元/件
![]()
解得![]()
∴生产![]() 种产品6件,生产
种产品6件,生产![]() 种产品4件.
种产品4件.
(2)设![]() 种产品
种产品![]() 件,
件,![]() 种产品
种产品![]() 件.
件.
![]()
∴![]() ,∴工厂共有4种生产方案:
,∴工厂共有4种生产方案:
方案一:![]() 种产品生产3件,
种产品生产3件,![]() 种产品生产7件;
种产品生产7件;
方案二:![]() 种产品生产4件,
种产品生产4件,![]() 种产品生产6件;
种产品生产6件;
方案三:![]() 种产品生产5件,
种产品生产5件,![]() 种产品生产5件;
种产品生产5件;
方案四:![]() 种产品生产6件,
种产品生产6件,![]() 种产品生产4件;
种产品生产4件;
(3)设所获利润为y,由(1)得![]() ,因为
,因为![]() ,所以y随x的增大而减小, 故方案一获利最大,最大利润为
,所以y随x的增大而减小, 故方案一获利最大,最大利润为![]() (万元)
(万元)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,美丽的弦图,蕴含着四个全等的直角三角形.已知每个直角三角形较长的直角边为a,较短的直角边为b,斜边长为c.如图②,现将这四个全图②等的直角三角形紧密拼接,形成飞镖状,已知外围轮廓(实线)的周长为24,OC=3,则该飞镖状图案的面积( )
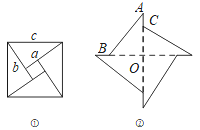
A. 6 B. 12 C. 24 D. 24
-
科目: 来源: 题型:
查看答案和解析>>【题目】使得函数值为零的自变量的值称为函数的零点.例如,对于函数y=x-1,令y=0可得x=1,我们就说1是函数y=x-1的零点.
已知y=x2-2mx-2(m+3)(m为常数).
(1)当m=0时,求该函数的零点;
(2)证明:无论m取何值,该函数总有两个零点;
(3)设函数的两个零点分别为x1和x2,且
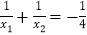 ,此时函数图象与x轴的交点分别为A,B(点A在点B左侧),点M在直线y=x-10上,当MA+MB最小时,求直线AM的函数表达式.
,此时函数图象与x轴的交点分别为A,B(点A在点B左侧),点M在直线y=x-10上,当MA+MB最小时,求直线AM的函数表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,三角形
 的三个顶点的位置如图,
的三个顶点的位置如图, 为三角形
为三角形 内一点,
内一点, 的坐标为
的坐标为
(1)平移三角形
 ,使
,使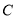 点与原点重合,请画出平移后的三角形
点与原点重合,请画出平移后的三角形
(2)直接写出
 的对应点
的对应点 的坐标;并写出平移的规律.
的坐标;并写出平移的规律. ( , );
( , ); ( , );
( , ); ( , );
( , );(3)求三角形
 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,四边形
 为长方形,其中点
为长方形,其中点 的坐标分别为
的坐标分别为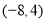 、
、 ,且
,且 轴,交
轴,交 轴于点
轴于点 ,
, 交
交 轴于点
轴于点 .
.(1)求
 两点坐标;
两点坐标;(2)一动点
 从
从 出发,以2个单位/秒的速度沿
出发,以2个单位/秒的速度沿 向
向 点运动(不与
点运动(不与 点重合),在
点重合),在 点运动过程中,连接
点运动过程中,连接 ,
,①试探究
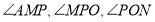 之间的数量关系;并说明理由;
之间的数量关系;并说明理由;②是否存在某一时刻
 ,使三角形
,使三角形 的面积等于长方形
的面积等于长方形 面积的
面积的 ?若存在,求
?若存在,求 的值并求此时点
的值并求此时点 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;③三角形
 的面积记作
的面积记作 ;三角形
;三角形 的面积记作
的面积记作 ;三角形
;三角形 的面积记作
的面积记作 ;直接写出
;直接写出 、
、 、
、 的关系.
的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以△ABC的一边AB为直径作⊙O,交AC,BC于D,E两点,若AB=4,∠BED=120°,点E是BD中点,则图中阴影部分的面积是( )

A. 4 B.
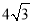 C.
C. 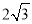 D.
D. 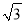
-
科目: 来源: 题型:
查看答案和解析>>【题目】五一小长假的某一天,亮亮全家上午
 时自驾小汽车从家里出发,到某旅游景点游玩,该小汽车离家的距离(千米)与时间(时)之间的关系如图所示,根据图像提供的有关信息,判断下列说法错误的是( )
时自驾小汽车从家里出发,到某旅游景点游玩,该小汽车离家的距离(千米)与时间(时)之间的关系如图所示,根据图像提供的有关信息,判断下列说法错误的是( )
A.景点离亮亮的家
 千米
千米B.亮亮到家的时间为
 时
时C.小汽车返程的速度为
 千米/时
千米/时D.
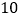 时至
时至 时,小汽车匀速行驶
时,小汽车匀速行驶
相关试题

