【题目】阅读下面材料:
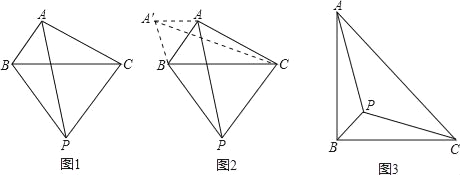
小伟遇到这样一个问题:如图1,在△ABC(其中∠BAC是一个可以变化的角)中,AB=2,AC=4,以BC为边在BC的下方作等边△PBC,求AP的最大值.
小伟是这样思考的:利用变换和等边三角形将边的位置重新组合.他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A′BC,连接A′A,当点A落在A′C上时,此题可解(如图2).
请你回答:AP的最大值是 .
参考小伟同学思考问题的方法,解决下列问题:
如图3,等腰Rt△ABC.边AB=4,P为△ABC内部一点,则AP+BP+CP的最小值是 .(结果可以不化简)
参考答案:
【答案】(1)6;(2)2![]() +2
+2![]() .
.
【解析】
(1)由旋转得到△A′BC,有△A′BA是等边三角形,当点A′A、C三点共线时,A′C=AA′+AC,最大即可;
(2)由旋转得到结论PA+PB+PC=P1A1+P1B+PC,只有,A1、P1、P、C四点共线时,(P1A+P1B+PC)最短,即线段A1C最短,根据勾股定理,即可.
(1)如图2,
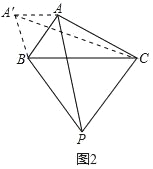
∵△ABP逆时针旋转60°得到△A′BC,
∴∠A′BA=60°,A′B=AB,AP=A′C
∴△A′BA是等边三角形,
∴A′A=AB=BA′=2,
在△AA′C中,A′C<AA′+AC,即AP<6,
则当点A′A、C三点共线时,A′C=AA′+AC,即AP=6,即AP的最大值是:6;
故答案是:6.
(2)如图3,
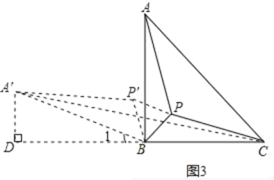
∵Rt△ABC是等腰三角形,∴AB=BC.
以B为中心,将△APB逆时针旋转60°得到△A'P'B.则A'B=AB=BC=4,PA=P′A′,PB=P′B,
∴PA+PB+PC=P′A′+P'B+PC.
∵当A'、P'、P、C四点共线时,(P'A+P'B+PC)最短,即线段A'C最短,
∴A'C=PA+PB+PC,
∴A'C长度即为所求.
过A'作A'D⊥CB延长线于D.
∵∠A'BA=60°(由旋转可知),
∴∠1=30°.
∵A'B=4,
∴A1D=2,BD=2![]()
∴CD=4+2![]() ;
;
在Rt△A1DC中,A1C=![]() .
.
∴AP+BP+CP的最小值是:![]() (或不化简为
(或不化简为![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于8个,所需费用总额不超过800元.请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方案
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,

(1)求高台A比矮台B高多少米?
(2)求旗杆的高度OM;
(3)玛丽在荡绳索过程中离地面的最低点的高度MN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
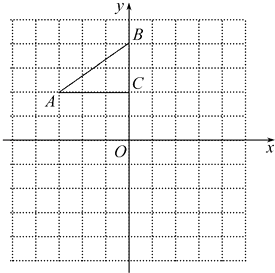
(1)将△ABC以点O为旋转中心旋转90°,请画出旋转后的△A′B′C′;
(2)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=10,AD=4,点P在边DC上,且△PAB是直角三角形,请在图中标出符合题意的点P,并直接写出PC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在长方形
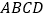 中,
中,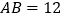 cm,
cm,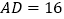 cm.现将其按下列步骤折叠:(1)将边
cm.现将其按下列步骤折叠:(1)将边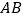 向边
向边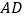 折叠,使边
折叠,使边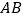 落在边
落在边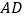 上,得到折痕
上,得到折痕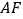 ,如图②;(2)将
,如图②;(2)将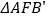 沿
沿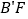 折叠,
折叠,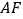 与
与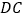 交于点
交于点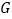 ,如图③.则所得梯形
,如图③.则所得梯形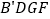 的周长等于( )
的周长等于( )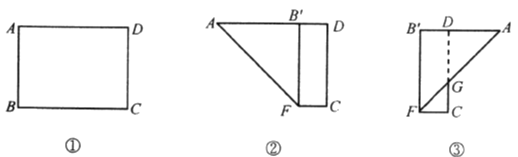
A.
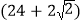 cm B.
cm B. 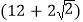 cm
cmC.
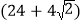 cm D.
cm D. 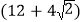 cm
cm -
科目: 来源: 题型:
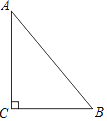
查看答案和解析>>【题目】如图是一块直角三角形的绿地,量得直角边BC为6cm,AC为8cm,现在要将原绿地扩充后成等腰三角形,且扩充的部分是以AC为直角边的直角三角形,求扩充后的等腰三角形绿地的周长.
相关试题

