【题目】如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交 ![]() 于点E,以点C为圆心,OA的长为直径作半圆交CE于点D.若OA=4,则图中阴影部分的面积为( )
于点E,以点C为圆心,OA的长为直径作半圆交CE于点D.若OA=4,则图中阴影部分的面积为( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】D
【解析】连接OE,
∵C为OA的中点,OC⊥OA且OA=4,
∴OC=2,
∴ ![]() ,
, ![]() .,
.,
∴cos∠COE=60°.
∵∠AOB=90°,
∴∠BOE=30°,
∴ ![]()
![]()
![]()
![]()
故答案为:D.
连接OE,得出S阴影=S扇形AOBS扇形ACDS扇形BOES△COE , 先根据已知求出OC的长,再在Rt△OCD中,利用三角函数的定义及特殊角的三角函数值求出∠COE的度数,从而求出∠BOE的度数,然后利用扇形的面积公式及三角形的面积公式分别求出扇形AOB、扇形ACD、扇形BOE、△COE的面积,即可求出答案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=4x2﹣2ax+b与x轴相交于A(x1 , 0),B(x2 , 0)(0<x1<x2)两点,与y轴交于点C.
(1)设AB=2,tan∠ABC=4,求该抛物线的解析式;
(2)在(1)中,若点D为直线BC下方抛物线上一动点,当△BCD的面积最大时,求点D的坐标;
(3)是否存在整数a,b使得1<x1<2和1<x2<2同时成立,请证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 的两条高
的两条高 交于点
交于点 ,点
,点 分别是
分别是 ,
, 的中点,连接
的中点,连接 .
.
 求证:
求证: 垂直平分
垂直平分 ;
; 若
若 .判断以
.判断以 为顶点的四边形的形状,并证明你的结论.
为顶点的四边形的形状,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程中,是一元二次方程的是( )
A.
B.
C.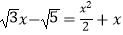
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】研究“掷一枚图钉,钉尖朝上”的概率,两个小组用同一个图钉做试验进行比较,他们的统计数据如下:
掷图钉的次数
50
100
200
300
400
钉尖朝上
的次数
第一小组
23
39
79
121
160
第二小组
24
41
81
124
164
(1)请你估计第一小组和第二小组所得的概率分别是多少?
(2)你认为哪一个小组的结果更准确?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△
 的位置,点B,O分别落在点
的位置,点B,O分别落在点  ,
,  处,点
处,点  在
在  轴上,再将△
轴上,再将△ 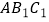 绕点
绕点  顺时针旋转到△
顺时针旋转到△  的位置,点
的位置,点  在
在  轴上,将△
轴上,将△  绕点
绕点  顺时针旋转△
顺时针旋转△  的位置,点
的位置,点  在
在  轴上……依次进行下去。若点
轴上……依次进行下去。若点  ,B(0,2),则点
,B(0,2),则点  的坐标为 .
的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2两图的阴影部分面积,可以得到乘法公式 (用式子表达);
(4)运用你所得到的公式,计算下列各题:
①(2m+n-p)(2m-n+p);②10.3×9.7.

相关试题

