【题目】如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.
①试说明BE·AD=CD·AE;
②根据图形特点,猜想![]() 可能等于哪两条线段的比?并证明你的猜想,(只须写出有线段的一组即可)
可能等于哪两条线段的比?并证明你的猜想,(只须写出有线段的一组即可)

参考答案:
【答案】(1)证明见解析;
(2)猜想![]() =
=![]() 或(
或(![]() 理由见解析
理由见解析
【解析】试题分析:
(1)由已知条件易证∠BAE=∠CAD,∠AEB=∠ADC,从而可得△AEB∽△ADC,由此可得![]() ,这样就可得到BE·AD=DC·AE;
,这样就可得到BE·AD=DC·AE;
(2)由(1)中所得△AEB∽△ADC可得![]() =
=![]() ,结合∠DAE=∠BAC可得△BAC∽△EAD,从而可得:
,结合∠DAE=∠BAC可得△BAC∽△EAD,从而可得: ![]() =
=![]() 或(
或(![]() ).
).
试题解析:
①∵∠BAC=∠DAE,
∴∠BAC+∠CAE=∠DAE+∠CAE,
即∠DAC=∠BAE,
∵∠AEB=∠ADB+∠DAE,
∠ADC=∠ADB+∠BDC,
又∵∠DAE=∠BDC,
∴∠AEB=∠ADC,
∴△BEA∽△CDA,
∴![]() =
=![]() ,
,
即BE·AD=CD·AE;
②猜想![]() =
=![]() 或(
或(![]() ),
),
由△BEA∽△CDA可知, ![]() =
=![]() ,即
,即![]() =
=![]() ,
,
又∵∠DAE=∠BAC,
∴△BAC∽△EAD,
∴![]() =
=![]() 或(
或(![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,把二元一次方程
 的一个解用一个点表示出来,例如:可以把它的其中一个解
的一个解用一个点表示出来,例如:可以把它的其中一个解 用点(2,1 )在平面直角坐标系中表示出来
用点(2,1 )在平面直角坐标系中表示出来探究1:
(1)请你在直角坐标系中标出4个以方程
 的解为坐标的点,然后过这些点中的任意两点作直线,你有什么发现,请写出你的发现 .
的解为坐标的点,然后过这些点中的任意两点作直线,你有什么发现,请写出你的发现 .在这条直线上任取一点,这个点的坐标是方程
 的解吗? (填“是”或“不是”___
的解吗? (填“是”或“不是”___(2)以方程
 的解为坐标的点的全体叫做方程
的解为坐标的点的全体叫做方程 的图象.根据上面的探究想一想:方程
的图象.根据上面的探究想一想:方程 的图象是_ _.
的图象是_ _.
探究2:根据上述探究结论,在同-平面直角坐标系中画出二元一次方程组
 中的两个二元一次方程的图象,由这两个二元一次方程的图象,请你直接写出二元一次方程组
中的两个二元一次方程的图象,由这两个二元一次方程的图象,请你直接写出二元一次方程组 的解,即
的解,即 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一副三角板
 和
和 拼合在一起,边
拼合在一起,边 与
与 重合,
重合, ,
, ,
, ,
, .当点
.当点 从点
从点 出发沿
出发沿 向下滑动时,点
向下滑动时,点 同时从点
同时从点 出发沿射线
出发沿射线 向右滑动.当点
向右滑动.当点 从点
从点 滑动到点
滑动到点 时,连接
时,连接 ,则
,则 的面积最大值为_______
的面积最大值为_______ .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AH∥CG,且分别交对角线BD于H、G,连接CH和AG,求证:∠CHG=∠AGH.

-
科目: 来源: 题型:
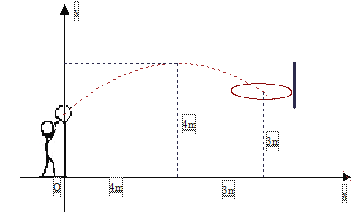
查看答案和解析>>【题目】初三年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高
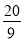 m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.(1)建立如图所示的平面直角坐标系,求抛物线的解析式并判断此球能否准确投中?
(2)此时,若对方队员乙在甲前面1m处跳起盖帽拦截,已知乙的最大摸高为3.1m,那么他能否获得成功?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,圆锥的母线长6cm,底面半径是3cm,在B处有一只蚂蚁,在AC中点P处有一颗米粒,蚂蚁从B爬到P处的最短距离是( )

A. 3
 cm B. 3
cm B. 3 cm C. 9cm D. 6cm
cm C. 9cm D. 6cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠ABE=20°,那么∠EFC′的度数为( )

A. 115° B. 120° C. 125° D. 130°
相关试题

