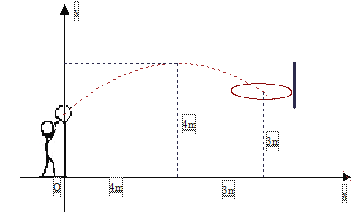
【题目】初三年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高![]() m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式并判断此球能否准确投中?
(2)此时,若对方队员乙在甲前面1m处跳起盖帽拦截,已知乙的最大摸高为3.1m,那么他能否获得成功?
参考答案:
【答案】(1)能够投中,理由见解析;(2)能够盖帽拦截成功.
【解析】试题分析:
(1)由题意可知抛物线经过(0, ![]() ),顶点坐标是(4,4),因此设抛物线的解析式为“顶点式”,代入两点坐标即可求得解析式;然后将篮圈的横坐标7代入解析式看对应的函数值是否等于篮圈的纵坐标即可判断能否投中;
),顶点坐标是(4,4),因此设抛物线的解析式为“顶点式”,代入两点坐标即可求得解析式;然后将篮圈的横坐标7代入解析式看对应的函数值是否等于篮圈的纵坐标即可判断能否投中;
(2)由题意将![]() 代入(1)中所求的解析式,看计算出的函数值是否小于或等于3.1,即可判断能否拦截成功.
代入(1)中所求的解析式,看计算出的函数值是否小于或等于3.1,即可判断能否拦截成功.
试题解析:
由题意可知,抛物线经过(0, ![]() ),顶点坐标是(4,4).
),顶点坐标是(4,4).
∴可设抛物线的解析式是![]() ,
,
代入点(0, ![]() ),得:
),得: ![]() ,解得
,解得![]() ,
,
∴抛物线的解析式是![]() ;
;
∵当![]() 时,
时, ![]() ,
,
∴代表篮圈的点(7,3)在抛物线上,
∴能够投中.
(2)∵当![]() 时,
时, ![]() <3.1,
<3.1,
∴乙能够盖帽拦截成功.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一副三角板
 和
和 拼合在一起,边
拼合在一起,边 与
与 重合,
重合, ,
, ,
, ,
, .当点
.当点 从点
从点 出发沿
出发沿 向下滑动时,点
向下滑动时,点 同时从点
同时从点 出发沿射线
出发沿射线 向右滑动.当点
向右滑动.当点 从点
从点 滑动到点
滑动到点 时,连接
时,连接 ,则
,则 的面积最大值为_______
的面积最大值为_______ .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AH∥CG,且分别交对角线BD于H、G,连接CH和AG,求证:∠CHG=∠AGH.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.
①试说明BE·AD=CD·AE;
②根据图形特点,猜想
 可能等于哪两条线段的比?并证明你的猜想,(只须写出有线段的一组即可)
可能等于哪两条线段的比?并证明你的猜想,(只须写出有线段的一组即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,圆锥的母线长6cm,底面半径是3cm,在B处有一只蚂蚁,在AC中点P处有一颗米粒,蚂蚁从B爬到P处的最短距离是( )

A. 3
 cm B. 3
cm B. 3 cm C. 9cm D. 6cm
cm C. 9cm D. 6cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠ABE=20°,那么∠EFC′的度数为( )

A. 115° B. 120° C. 125° D. 130°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
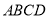 中,
中, ,
, ,点
,点 是
是 边的中点,点
边的中点,点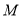 是
是 边上一动点(不与点
边上一动点(不与点 重合),延长
重合),延长 交射线
交射线 于点
于点 ,连接
,连接 ,
,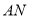 .
.
(1)求证:四边形
 是平行四边形;
是平行四边形;(2)填空:
①当
 的值为_______时,四边形
的值为_______时,四边形 是矩形;
是矩形;②当
 的值为______时,四边形
的值为______时,四边形 是菱形.
是菱形.
相关试题

