【题目】为了争创全国文明卫生城市,优化城市环境,节约能源,某市公交公司决定购买一批共10台全新的混合动力公交车,现有A、B两种型号,其中每台的价格,年省油量如下表:
A | B | |
价格(万元/台) | a | b |
节省的油量(万升/年) | 2.4 | 2 |
经调查,购买一台A型车比购买一台B型车多10万元,购买3台A型车比购买4台B型车少30万元.
(1)请求出a和b的值;
(2)若购买这批混合动力公交车(两种车型都要有)每年能节省的油量不低于21.6万升,请问有几种购车方案?请写出解答过程.
(3)求(2)中最省钱的购车方案及所需的购车款.
参考答案:
【答案】(1)a、b的值分别是70、60;(2)共有6种购车方案,解答过程见解析; (3)购买A型车4辆,B型车6辆,所需的购车款是640万元.
【解析】
(1)根据题意可列出关于a,b的方程组,解方程组即可;
(2)设购买A型公交车x辆,则购买B型公交车(10﹣x)辆,根据“购买这批混合动力公交车(两种车型都要有)每年能节省的油量不低于21.6万升”列出不等式,解出不等式,同时注意两种车型都要有,最终确定x的取值范围,然后根据x为正整数可确定x的取值有6种;
(3)设购车款为w万元,购买A型车x辆,先根据题意找到w与x之间的关系式,然后根据一次函数的性质即可得出答案
(1)由题意可得:
![]() ,解得:
,解得:![]() ,
,
答:a、b的值分别是70、60;
(2)设购买A型公交车x辆,则购买B型公交车(10﹣x)辆.
由题意可得:
2.4x+2(10﹣x)≥21.6,解得,x≥4,
∵两种车型都要有,
∴![]() ,
,
∴4≤x<10,
∵x为整数,
∴x=4、5、6、7、8、9,
∴共有6种购车方案.
(3)设购车款为w万元,购买A型车x辆,由题意可得:
w=70x+60(10﹣x)=10x+600,(4≤x<10且x为整数)
∵10>0
∴w随x的增大而增大
∴当x=4时,w取得最小值,此时w最小值=640(万元),
答:(2)中最省钱的购买方案为:购买A型车4辆,B型车6辆,所需的购车款是640万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,BC=8,点P由点B向点A运动,同时,点Q由点C出发沿线段AC的延长线运动,已知点P、Q运动速度相等,点Q与线段BC相交于点D,过点P作PE∥AQ,交BC于点E.
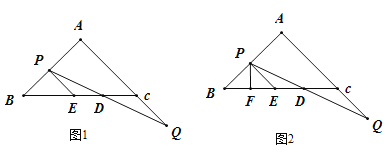
(1)如图1,求证:D为CE中点;
(2)如图2,过点P作PF⊥BC,垂足为点F,在P、Q的运动过程中,请判断DF的长度是否为定值;若是,请求出DF的长度;若否,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论,其中不正确的是( )
A. 当m=﹣3时,函数图象的顶点坐标是(
 ,
, )
)B. 当m>0时,函数图象截x轴所得的线段长度大于

C. 当m≠0时,函数图象经过同一个点
D. 当m<0时,函数在x>
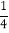 时,y随x的增大而减小
时,y随x的增大而减小 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰Rt△ABC中,∠C=90°,点O是AB的中点,边AC的长为6,将一块边长足够长的三角板的直角顶点放在O点处,将三角板绕着点O旋转,始终保持三角板的直角边与AC相交,交点为点D,另一条直角边与BC相交,交点为点E,则等腰直角三角形ABC的边被三角板覆盖部分的两条线段CD与CE长度之和为( )
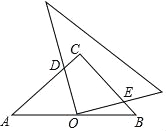
A. 7 B. 6 C. 5 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
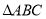 中,
中,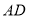 是高线,过点
是高线,过点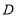 作
作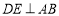 于点
于点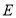 ,
,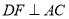 于点
于点 ,且
,且 ,则下列判断中不正确的是( )
,则下列判断中不正确的是( )
A.
 是
是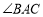 的平分线B.
的平分线B.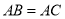
C.
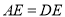 D.图中有
D.图中有 对全等三角形
对全等三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】 如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列结论错误的是( ).
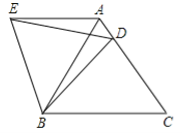
A.AE∥BC B. ∠ADE=∠BDC
C.△BDE是等边三角形 D. △ADE的周长是9
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
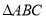 中,
中,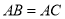 ,
,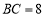 ,点
,点 从点
从点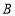 出发沿射线
出发沿射线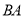 移动,同时点
移动,同时点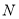 从点
从点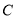 出发沿线段
出发沿线段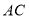 的延长线移动,点
的延长线移动,点 ,
,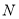 移动的速度相同,
移动的速度相同,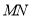 与
与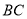 相交于点
相交于点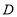 .
.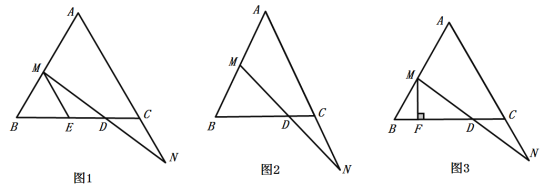
(1)如图1,过点
 作
作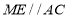 ,交
,交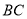 于点
于点 ,求证:
,求证: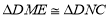 ;
;(2)如图2,
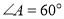 ,当点
,当点 移动到
移动到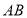 的中点时,求
的中点时,求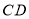 的长度;
的长度;(3)如图3,过点
 作
作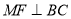 于点
于点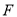 .在点
.在点 从点
从点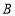 向点
向点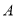 (点
(点 不与点
不与点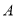 ,
,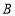 重合)移动的过程中,线段
重合)移动的过程中,线段 与
与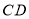 的长度是否保持不变若保持不变,请求出
的长度是否保持不变若保持不变,请求出 与
与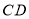 的长度和;若改变,请说明理由.
的长度和;若改变,请说明理由.
相关试题

