【题目】《九章算术》中记载了这样一道题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代的语言表述为:“如果AB为⊙O的直径,弦CD⊥AB于E,AE=1寸,CD=10寸,那么直径AB的长为多少寸?”请你补全示意图,并求出AB的长. 
参考答案:
【答案】解:如图所示,连接OD.
∵弦CD⊥AB,AB为圆O的直径,
∴E为CD的中点,
又∵CD=10寸,
∴CE=DE= ![]() CD=5寸,
CD=5寸,
设OD=OA=x寸,则AB=2x寸,OE=(x﹣1)寸,
由勾股定理得:OE2+DE2=OD2 ,
即(x﹣1)2+52=x2 ,
解得:x=13,
∴AB=26寸,
即直径AB的长为26寸.
【解析】连接OD,由直径AB与弦CD垂直,根据垂径定理得到E为CD的中点,由CD的长求出DE的长,设OD=OA=x寸,则AB=2x寸,OE=(x﹣1)寸,由勾股定理得出方程,解方程求出半径,即可得出直径AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示.

(1)求这个二次函数的解析式;
(2)根据图象,写出当x取何值时,y>0? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:
①两个数互为倒数,则它们的乘积为
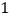 ;②若
;②若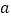 ,
,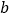 互为相反数,则
互为相反数,则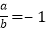 ;
;③
 个有理数相乘,如果负因数的个数为奇数个,则积为负;④若
个有理数相乘,如果负因数的个数为奇数个,则积为负;④若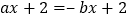 ,则
,则 .其中正确的个数为( )
.其中正确的个数为( )A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的正方形ABCD中,对角线AC,BD相交于点O,点E是AD边上一点,连接CE,把△CDE沿CE翻折,得到△CPE,EP交AC于点F,CP交BD于点G,连接PO,若PO∥BC,则四边形OFPG的面积是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】图①是一块边长为1,周长记为P1的正三角形纸板,沿图①的底边剪去一块边长为
 的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪如图掉正三角形纸板边长的
的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪如图掉正三角形纸板边长的 )后,得图③,④,…,记第n(n≥3)块纸板的周长为Pn,则P2018﹣P2017的值为( )
)后,得图③,④,…,记第n(n≥3)块纸板的周长为Pn,则P2018﹣P2017的值为( )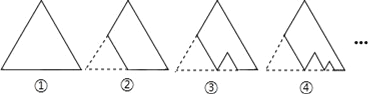
A.
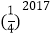 B.
B. 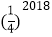 C.
C. 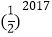 D.
D. 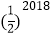
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在数轴上点A表示数a,点B表示数b,且a,b满足
 .
.(1)点A表示的数为________,点B表示的数为________;
(2)设点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.若在数轴上存在一点C,使BC=2AC,则点C表示的数为__________;
(3)若在原点处放一挡板,一小球甲从点A处以每秒2个单位长度的速度向左运动;同时另一小球乙从点B以每秒2个单位长度的速度也向左运动,在碰到挡板后(忽略球的大小,可看做一点)以原来速度的两倍向相反的方向运动.设运动的时间为t秒,请用含t的代数式分别表示出甲、乙两小球到原点的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣2x﹣3.
(1)将y=x2﹣2x﹣3化成y=a(x﹣h)2+k的形式;
(2)与y轴的交点坐标是 , 与x轴的交点坐标是;
(3)在坐标系中利用描点法画出此抛物线.x
…
…
y
…
…
(4)不等式x2﹣2x﹣3>0的解集是 .
相关试题

