【题目】已知,在数轴上点A表示数a,点B表示数b,且a,b满足![]() .
.
(1)点A表示的数为________,点B表示的数为________;
(2)设点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.若在数轴上存在一点C,使BC=2AC,则点C表示的数为__________;
(3)若在原点处放一挡板,一小球甲从点A处以每秒2个单位长度的速度向左运动;同时另一小球乙从点B以每秒2个单位长度的速度也向左运动,在碰到挡板后(忽略球的大小,可看做一点)以原来速度的两倍向相反的方向运动.设运动的时间为t秒,请用含t的代数式分别表示出甲、乙两小球到原点的距离.
参考答案:
【答案】(1)-2,4(2)0或-8(3)2t+2;4-2t或4t-8
【解析】
(1)根据非负数的性质求得a=-2,b=4;
(2)根据两点间距离的表示列出绝对值方程,然后求解即可;
(3)①甲球到原点的距离=甲球运动的路程+OA的长,乙球到原点的距离分两种情况:(Ⅰ)当0<t≤2时,乙球从点B处开始向左运动,一直到原点O,此时OB的长度-乙球运动的路程即为乙球到原点的距离;(Ⅱ)当t>2时,乙球从原点O处开始向右运动,此时乙球运动的路程-OB的长度即为乙球到原点的距离;
(1)由题意得,a+2=0,b-4=0,
解得a=-2,b=4,
所以,点A表示-2,点B表示4;
(2)设点C表示x,由题意得,|4-x|=2|-2-x|,
所以,4-x=-2(-2-x)或4-x=2(-2-x),
解得x=0,或x=-8,
所以,点C表示的数为0或-8;
(3)甲:∵小球甲从点A处以2个单位/秒的速度向左运动,
∴甲到原点的距离为|-2-2t|=2t+2,
∵小球乙从点B处以2个单位/秒的速度也向左运动,
∴乙到达原点的时间为4÷2=2,
∴当0≤t≤2时,小球到原点的距离为4-2t,
当t>2时小球到原点的距离为4(t-2)=4t-8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的正方形ABCD中,对角线AC,BD相交于点O,点E是AD边上一点,连接CE,把△CDE沿CE翻折,得到△CPE,EP交AC于点F,CP交BD于点G,连接PO,若PO∥BC,则四边形OFPG的面积是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》中记载了这样一道题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代的语言表述为:“如果AB为⊙O的直径,弦CD⊥AB于E,AE=1寸,CD=10寸,那么直径AB的长为多少寸?”请你补全示意图,并求出AB的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】图①是一块边长为1,周长记为P1的正三角形纸板,沿图①的底边剪去一块边长为
 的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪如图掉正三角形纸板边长的
的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪如图掉正三角形纸板边长的 )后,得图③,④,…,记第n(n≥3)块纸板的周长为Pn,则P2018﹣P2017的值为( )
)后,得图③,④,…,记第n(n≥3)块纸板的周长为Pn,则P2018﹣P2017的值为( )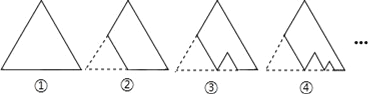
A.
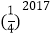 B.
B. 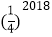 C.
C. 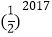 D.
D. 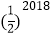
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣2x﹣3.
(1)将y=x2﹣2x﹣3化成y=a(x﹣h)2+k的形式;
(2)与y轴的交点坐标是 , 与x轴的交点坐标是;
(3)在坐标系中利用描点法画出此抛物线.x
…
…
y
…
…
(4)不等式x2﹣2x﹣3>0的解集是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是等边△ABC内的一点,且PA=5,PB=4,PC=3,将△APB绕点B逆时针旋转,得到△CQB.求:

(1)点P与点Q之间的距离;
(2)求∠BPC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某蒜薹生产基地喜获丰收,收获蒜薹200吨.经市场调查,可采用批发、零售、冷库储藏后销售三种方式,并按这三种方式销售,计划平均每吨的售价及成本如下表:
销售方式
批发
零售
储藏后销售
售价(元/吨)
3000
4500
5500
成本(元/吨)
700
1000
1200
若经过一段时间,蒜薹按计划全部售出获得的总利润为y(元),蒜薹零售x(吨),且零售量是批发量的
 .
.(1)求y与x之间的函数关系式;
(2)由于受条件限制,经冷库储藏售出的蒜薹最多80吨,求该生产基地按计划全部售完蒜薹获得的最大利润.
相关试题

