【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上的一个动点,作
上的一个动点,作![]() ,且
,且![]() ,连接
,连接![]() 交射线
交射线![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() _______.
_______.
参考答案:
【答案】4或6
【解析】
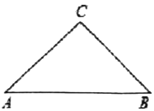
过点F作FD⊥AC,交AC于点D,根据∠ADF=∠C=90°,∠AFD=∠EAD,AF=AE,证明△AFD≌△EAC,则FD=AC=BC,AD=CE,又证明△FDG≌△BCG,得到CG=DG,由![]() ,设BC=5x,BE=2x;由点E是动点,则①当点E在BC线段之间时,CE=AD=3x,则AG=4x,CG=x,此时
,设BC=5x,BE=2x;由点E是动点,则①当点E在BC线段之间时,CE=AD=3x,则AG=4x,CG=x,此时![]() 4;①当点E在CB的延长线上时,CE=AD=7x,则AG=6x,CG=DG=x,此时
4;①当点E在CB的延长线上时,CE=AD=7x,则AG=6x,CG=DG=x,此时![]() 6;即可得到答案.
6;即可得到答案.
解:根据题意作出图形,过点F作FD⊥AC,交AC于点D,
∴∠ADF=∠C=90°,
∵AF⊥AE,
∴∠FAE=90°,
∴∠FAD+∠EAD=90°,
∵∠FAD+∠AFD=90°,
∴∠EAD=∠AFD,
∵AF=AE,
∴△AFD≌△EAC(AAS),
∴FD=AC=BC,AD=CE,
∵∠DGF=∠CGB,
∴△FDG≌△BCG,
∴CG=DG;
∵由![]() ,设BC=AC=5x,BE=2x,
,设BC=AC=5x,BE=2x,
由点E是动点,则①当点E在BC线段之间时,如图:

∴CE=AD=3x,
∴CG=DG=x,
∴AG=4x,
∴![]() ;
;
②当点E在CB的延长线上时,如图:

∴CE=AD=7x,
∴CG=DG=x,
∴AG=6x,
∴![]() ;
;
故答案为:4或6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们生活水平的不断提高,人们对生活饮用水质量要求也越来越高,更多的居民选择购买家用净水器.一商家抓住商机,从生产厂家购进了
 ,
, 两种型号家用净水器.已知购进2台
两种型号家用净水器.已知购进2台 型号家用净水器比1台
型号家用净水器比1台 型号家用净水器多用200元;购进3台
型号家用净水器多用200元;购进3台 型号净水器和2台
型号净水器和2台 型号家用净水器共用6600元
型号家用净水器共用6600元(1)求
 ,
, 两种型号家用净水器每台进价各为多少元?
两种型号家用净水器每台进价各为多少元?(2)该商家用不超过26400元共购进
 ,
, 两种型号家用净水器20台,再将购进的两种型号家用净水器分别加价
两种型号家用净水器20台,再将购进的两种型号家用净水器分别加价 后出售,若两种型号家用净水器全部售出后毛利润不低于12000元,求商家购进
后出售,若两种型号家用净水器全部售出后毛利润不低于12000元,求商家购进 ,
, 两种型号家用净水器各多少台?(注:毛利润
两种型号家用净水器各多少台?(注:毛利润 售价
售价 进价)
进价) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1.将三角板中30°角的顶点D放在AB边上移动,使这个30°角的两边分别与△ABC的边AC,BC相交于点E,F,且使DE始终与AB垂直.

(1)△BDF是什么三角形?请说明理由;
(2)设AD=x,CF=y,试求y与x之间的函数关系式;(不用写出自变量x的取值范围)
(3)当移动点D使EF∥AB时,求AD的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
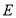 在等边
在等边 的边
的边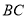 上,
上,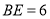 ,射线
,射线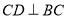 于点
于点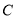 ,点
,点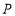 是射线
是射线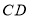 上一动点,点
上一动点,点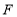 是线段
是线段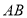 上一动点,当
上一动点,当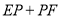 的值最小时,
的值最小时, ,则
,则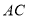 为( )
为( )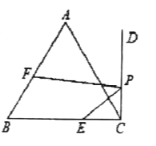
A. 14B. 13C. 12D. 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】班级组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有90公里,队伍8:00从学校出发.苏老师因有事情,8:30从学校自驾小车以大巴1.5倍的速度追赶,追上大巴后继续前行,结果比队伍提前15分钟到达基地.问:
(1)大巴与小车的平均速度各是多少?
(2)苏老师追上大巴的地点到基地的路程有多远?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,过点D作FG⊥AC于点F,交AB的延长线于点G.
(1)求证:FG是⊙O的切线;
(2)若tanC=2,求
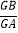 的值.
的值.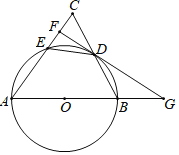
-
科目: 来源: 题型:
查看答案和解析>>【题目】
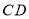 是
是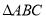 的高.
的高.(1)如图1,若
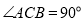 ,
,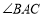 的平分线
的平分线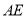 交
交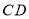 于点
于点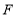 ,交
,交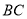 于点
于点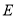 ,求证:
,求证: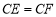 ;
;(2)如图2,若
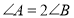 ,
,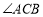 的平分线
的平分线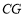 交
交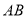 于点
于点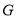 ,求
,求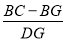 的值;
的值;(3)如图3,若
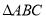 是以
是以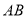 为斜边的等腰直角三角形,再以
为斜边的等腰直角三角形,再以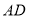 为斜边作等腰
为斜边作等腰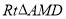 ,
,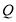 是
是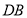 的中点,连接
的中点,连接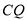 、
、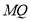 ,试判断线段
,试判断线段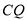 与
与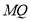 的关系,并给出证明.
的关系,并给出证明.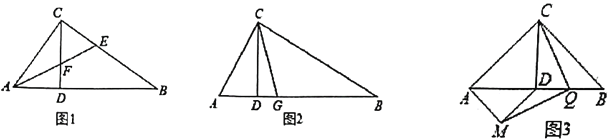
相关试题

