【题目】随着人们生活水平的不断提高,人们对生活饮用水质量要求也越来越高,更多的居民选择购买家用净水器.一商家抓住商机,从生产厂家购进了![]() ,
,![]() 两种型号家用净水器.已知购进2台
两种型号家用净水器.已知购进2台![]() 型号家用净水器比1台
型号家用净水器比1台![]() 型号家用净水器多用200元;购进3台
型号家用净水器多用200元;购进3台![]() 型号净水器和2台
型号净水器和2台![]() 型号家用净水器共用6600元
型号家用净水器共用6600元
(1)求![]() ,
,![]() 两种型号家用净水器每台进价各为多少元?
两种型号家用净水器每台进价各为多少元?
(2)该商家用不超过26400元共购进![]() ,
,![]() 两种型号家用净水器20台,再将购进的两种型号家用净水器分别加价
两种型号家用净水器20台,再将购进的两种型号家用净水器分别加价![]() 后出售,若两种型号家用净水器全部售出后毛利润不低于12000元,求商家购进
后出售,若两种型号家用净水器全部售出后毛利润不低于12000元,求商家购进![]() ,
,![]() 两种型号家用净水器各多少台?(注:毛利润
两种型号家用净水器各多少台?(注:毛利润![]() 售价
售价![]() 进价)
进价)
参考答案:
【答案】(1)![]() 型号家用净水器每台进价为1000元,
型号家用净水器每台进价为1000元,![]() 型号家用净水器每台进价为1800元;(2)
型号家用净水器每台进价为1800元;(2)
则商家购进![]() 型号家用净水器12台,购进
型号家用净水器12台,购进![]() 型号家用净水器8台;购进
型号家用净水器8台;购进![]() 型号家用净水器13
型号家用净水器13
台,购进![]() 型号家用净水器7台;购进
型号家用净水器7台;购进![]() 型号家用净水器14台,购进
型号家用净水器14台,购进![]() 型号家用净水器6台;
型号家用净水器6台;
购进![]() 型号家用净水器15台,购进
型号家用净水器15台,购进![]() 型号家用净水器5台.
型号家用净水器5台.
【解析】
(1)设A型号家用净水器每台进价为x元,B型号家用净水器每台进价为y元,根据“购进2台A型号家用净水器比1台B型号家用净水器多用200元;购进3台A型号净水器和2台B型号家用净水器共用6600元”列二元一次方程组求解可得;
(2)设商家购进A型号家用净水器m台,则购进B型号家用净水器(20-m)台,根据“购进总费用不超过26400元、毛利润不低于12000元”列不等式组,注意不超过是小于等于,不低于是大于等于,列出不等式组,解之可得.
【解】:(1)设![]() 型号家用净水器每台进价为
型号家用净水器每台进价为![]() 元,
元,![]() 型号家用净水器每台进价为
型号家用净水器每台进价为![]() 元,
元,
根据题意知![]() ,
,
解得:![]() ,
,
答:![]() 型号家用净水器每台进价为1000元,
型号家用净水器每台进价为1000元,![]() 型号家用净水器每台进价为1800元;
型号家用净水器每台进价为1800元;
(2)设商家购进![]() 型号家用净水器
型号家用净水器![]() 台,则购进
台,则购进![]() 型号家用净水器
型号家用净水器![]() 台,
台,
根据题意,得:![]() ,
,
解得:![]() ,
,
因为![]() 为整数,
为整数,
所以![]() 或13或14或15,
或13或14或15,
则商家购进![]() 型号家用净水器12台,购进
型号家用净水器12台,购进![]() 型号家用净水器8台;
型号家用净水器8台;
购进![]() 型号家用净水器13台,购进
型号家用净水器13台,购进![]() 型号家用净水器7台;
型号家用净水器7台;
购进![]() 型号家用净水器14台,购进
型号家用净水器14台,购进![]() 型号家用净水器6台;
型号家用净水器6台;
购进![]() 型号家用净水器15台,购进
型号家用净水器15台,购进![]() 型号家用净水器5台.
型号家用净水器5台.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个小组同时从甲地出发,匀速步行到乙地,甲乙两地相距7500米,第一组的步行速度是第二组的1.2倍,并且比第二组早15分钟到达乙地.设第二组的步行速度为x千米/小时,根据题意可列方程是( )
A. ﹣
﹣  =15
=15
B. ﹣
﹣  =
= 
C. ﹣
﹣  =15
=15
D. ﹣
﹣  =
= 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )

A.13
B.14
C.15
D.16 -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共8台,具体情况如下表:
A型
B型
价格(万元/台)
12
10
月污水处理能力(吨/月)
200
160
经预算,企业最多支出89万元购买设备,且要求月处理污水能力不低于1380吨.
(1)该企业有几种购买方案?
(2)哪种方案更省钱,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为响应党的“文化自信”号召,某校开展了古诗词诵读大赛活动,现随机抽取部分同学的成绩进行统计,并绘制成如下的两个不完整的统计图,请结合图中提供的信息,解答下列问题:
(1)
 _____,并把频数分布直方图补充完整;
_____,并把频数分布直方图补充完整;(2)求扇形
 的圆心角度数,成绩众数落在多少分之间;
的圆心角度数,成绩众数落在多少分之间;(3)如果全校有2000名学生参加这次活动,90分以上(含90分)为优秀,那么估计获得优秀奖的学生有多少人?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进30海里到达B点,此时,测得海岛C位于北偏东30°的方向,求海岛C到航线AB的距离CD的长(结果保留根号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:有些代数恒等式可以利用平面图形的面积来表示,如:
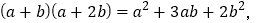 就可以用如图所示的面积关系来说明。
就可以用如图所示的面积关系来说明。(1)请根据如图写出代数恒等式,并根据所写恒等式计算:
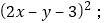
(2)若
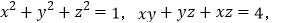 求
求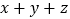 的值;
的值;(3)现有如图中的彩色卡片:A型、B型、C型,把这些卡片不重叠不留缝隙地贴在棱长为
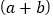 的100个立方体表面进行装饰,A型、B型、C型卡片的单价分别为0.7元/张、0.5元/张、0.4元/张,共需多少费用?
的100个立方体表面进行装饰,A型、B型、C型卡片的单价分别为0.7元/张、0.5元/张、0.4元/张,共需多少费用?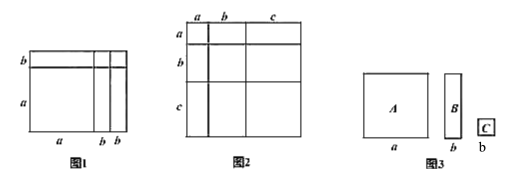
相关试题

