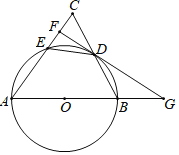
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,过点D作FG⊥AC于点F,交AB的延长线于点G.
(1)求证:FG是⊙O的切线;
(2)若tanC=2,求![]() 的值.
的值.
参考答案:
【答案】(1)证明见解析;(2)BG:GA=1:4.
【解析】(1)欲证明FG是⊙O的切线,只要证明OD⊥FG即可;
(2)由△GDB∽△GAD,设BG=a.可得![]() ,推出DG=2a,AG=4a,由此即可解决问题.
,推出DG=2a,AG=4a,由此即可解决问题.
(1)如图,连接AD、OD,
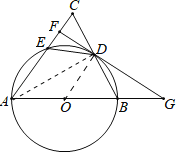
∵AB是直径,
∴∠ADB=90°,即AD⊥BC,
∵AC=AB,
∴CD=BD,
∵OA=OB,
∴OD∥AC,
∵DF⊥AC,
∴OD⊥DF,
∴FG是⊙O的切线;
(2)∵tanC=![]() =2,BD=CD,
=2,BD=CD,
∴BD:AD=1:2,
∵∠GDB+∠ODB=90°,∠ADO+∠ODB=90°,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠GDB=∠GAD,
∵∠G=∠G,
∴△GDB∽△GAD,设BG=a.
∴![]() ,
,
∴DG=2a,AG=4a,
∴BG:GA=1:4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
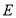 在等边
在等边 的边
的边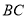 上,
上,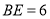 ,射线
,射线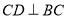 于点
于点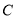 ,点
,点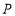 是射线
是射线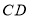 上一动点,点
上一动点,点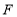 是线段
是线段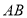 上一动点,当
上一动点,当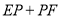 的值最小时,
的值最小时, ,则
,则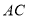 为( )
为( )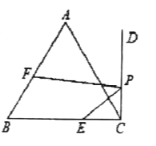
A. 14B. 13C. 12D. 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
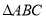 中,
中,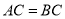 ,
,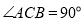 ,点
,点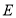 是射线
是射线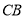 上的一个动点,作
上的一个动点,作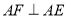 ,且
,且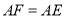 ,连接
,连接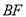 交射线
交射线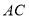 于点
于点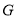 ,若
,若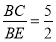 ,则
,则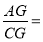 _______.
_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】班级组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有90公里,队伍8:00从学校出发.苏老师因有事情,8:30从学校自驾小车以大巴1.5倍的速度追赶,追上大巴后继续前行,结果比队伍提前15分钟到达基地.问:
(1)大巴与小车的平均速度各是多少?
(2)苏老师追上大巴的地点到基地的路程有多远?
-
科目: 来源: 题型:
查看答案和解析>>【题目】
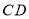 是
是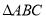 的高.
的高.(1)如图1,若
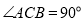 ,
,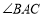 的平分线
的平分线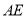 交
交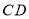 于点
于点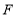 ,交
,交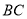 于点
于点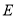 ,求证:
,求证: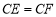 ;
;(2)如图2,若
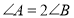 ,
,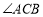 的平分线
的平分线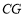 交
交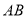 于点
于点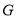 ,求
,求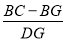 的值;
的值;(3)如图3,若
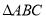 是以
是以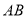 为斜边的等腰直角三角形,再以
为斜边的等腰直角三角形,再以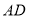 为斜边作等腰
为斜边作等腰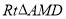 ,
,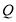 是
是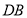 的中点,连接
的中点,连接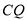 、
、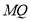 ,试判断线段
,试判断线段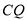 与
与 的关系,并给出证明.
的关系,并给出证明.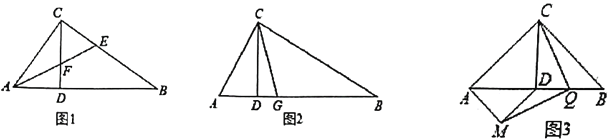
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=
 x2+bx+c经过点A(﹣2,0),B(0、﹣4)与x轴交于另一点C,连接BC.
x2+bx+c经过点A(﹣2,0),B(0、﹣4)与x轴交于另一点C,连接BC.(1)求抛物线的解析式;
(2)如图,P是第一象限内抛物线上一点,且S△PBO=S△PBC,求证:AP∥BC;
(3)在抛物线上是否存在点D,直线BD交x轴于点E,使△ABE与以A,B,C,E中的三点为顶点的三角形相似(不重合)?若存在,请求出点D的坐标;若不存在,请说明理由.
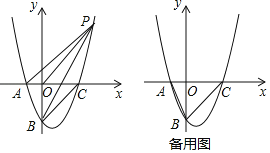
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD与正方形CEFG,M是AF的中点,连接DM,EM.
(1)如图1,点E在CD上,点G在BC的延长线上,请判断DM,EM的数量关系与位置关系,并直接写出结论;
(2)如图2,点E在DC的延长线上,点G在BC上,(1)中结论是否仍然成立?请证明你的结论;
(3)将图1中的正方形CEFG绕点C旋转,使D,E,F三点在一条直线上,若AB=13,CE=5,请画出图形,并直接写出MF的长.

相关试题

