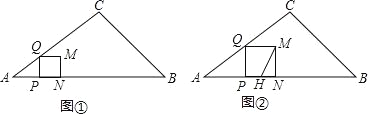
【题目】如图①，在△ABC中，AB=7，tanA=
，∠B=45°．点P从点A出发，沿AB方向以每秒1个单位长度的速度向终点B运动（不与点A、B重合），过点P作PQ⊥AB．交折线AC-CB于点Q，以PQ为边向右作正方形PQMN，设点P的运动时间为t（秒），正方形PQMN与△ABC重叠部分图形的面积为S（平方单位）．
（1）直接写出正方形PQMN的边PQ的长（用含t的代数式表示）．
（2）当点M落在边BC上时，求t的值．
（3）求S与t之间的函数关系式．
（4）如图②，点P运动的同时，点H从点B出发，沿B-A-B的方向做一次往返运动，在B-A上的速度为每秒2个单位长度，在A-B上的速度为每秒4个单位长度，当点H停止运动时，点P也随之停止，连结MH．设MH将正方形PQMN分成的两部分图形面积分别为S1、S2（平方单位）（0＜S1＜S2），直接写出当S2≥3S1时t的取值范围．
【答案】(1) PQ=7-t．(2) t=
．(3) 当0＜t≤时，S=
．当＜t≤4，
．当4＜t＜7时， 
．（4）
或
或
．
【解析】
试题分析：（1）分两种情况讨论：当点Q在线段AC上时，当点Q在线段BC上时．
（2）根据AP+PN+NB=AB，列出关于t的方程即可解答；
（3）当0＜t≤时，当＜t≤4，当4＜t＜7时；
（4）或或．
试题解析：（1）当点Q在线段AC上时，PQ=tanAAP=
t．
当点Q在线段BC上时，PQ=7-t．
（2）当点M落在边BC上时，如图③，
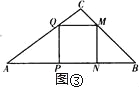
由题意得：t+t+t=7，
解得：t=．
∴当点M落在边BC上时，求t的值为．
（3）当0＜t≤时，如图④，
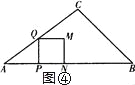
S=
．
当＜t≤4，如图⑤，
．
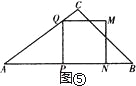
当4＜t＜7时，如图⑥，
．
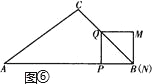
（4）或或．．
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】将背面完全相同，正面分别写有数字-2、1、-4的三张卡片混合后，小峰从中随机抽取一张，把卡片上的数字作为积的一个因式．将形状、大小完全相同，分别标有数字-1、3、4的三个小球混合后，小华随机抽取一个，把小球上的数字作为积的另一个因式，然后计算这两个数的乘积．
（1）请用列表法或画树状图的方法求出两个数的乘积是非负数的概率．
（2）小峰和小华做游戏，规则是：若这两数的积是非负数，则小峰赢；否则小华赢．你认为这个游戏公平吗？请说明理由，如果不公平，请你修改游戏规则，使游戏公平．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】关于二次函数y=ax2+bx+c图象有下列命题：
（1）当c=0时，函数的图象经过原点；
（2）当c＞0时，函数的图象开口向下时，方程ax2+bx+c=0必有两个不等实根；
（3）当b=0时，函数图象关于原点对称．
其中正确的个数有（ ）
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个容器装有一个注水管和两个排水管，每个排水管每分钟排水7.5L，从某一时刻开始2min内只注水不排水，2min后开启一个排水管，容器内的水量y（L）与注水时间x（min）之间的函数关系如图所示．
（1）求a的值．
（2）当2≤x≤6时，求y与x的函数关系式．
（3）若在6min之后，两个出水管均开启，注水管关闭，还需多长时间可排尽容器中的水？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，李明在自家楼房的窗口A处，测量楼前的路灯CD的高度，现测得窗口处A到路灯顶部C的仰角为44°，到地面的距离AB为20米，楼底到路灯的距离BD为12米，求路灯CD的高度（结果精确到0.1）
【参考数据：sin44°=0.69，cos44°=0.72，tan44°=0.97】
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校团委为了了解学生孝敬父母的情况，在全校范围内随机抽取n名学生进行问卷调查．问卷中孝敬父母方式包括：A．为父母洗一次脚；B．帮父母做一次家务；C．给父母买一件礼物；D．其他．每位学生在问卷调查时都按要求只选择了其中一种方式，该校团委收回全部问卷后，将收集到的数据整理并绘制成如下的统计图．
（1）求n的值．
（2）四种方式中被选择次数最多的方式为 （用A、B、C、D作答）；选择该种方式的学生人数占被调查的学生人数的百分比为 ．
（3）根据统计结果，估计该校1600名学生中选择B方式的学生比选择A方式的学生多的人数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com