【题目】一组数据15、13、14、13、16、13的众数是______,中位数是______.
参考答案:
【答案】13 13.5
【解析】
这组数据中出现次数最多的数为众数;把这组数按从小到大的顺序排列,因为数的个数是偶数个,那么中间两个数的平均数即是中位数由此解答.
解:∵15、13、14、13、16、13中13出现次数最多有3次,
∴众数为13,
将这组数从小到大排列为:13,13,13,14,15,16,最中间的两个数是13,14,所以中位数=(13+14)÷2=13.5
故答案为:13;13.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程(m+3)x2+4x+m2+2m-3=0有一个根为0,则m=______,另一根为________
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“两直线平行,同位角相等”的题设是_________;结论是_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列一元二次方程中,没有实数根的是( )
A. 4x2﹣5x+2=0 B. x2﹣6x+9=0 C. 5x2﹣4x﹣1=0 D. 3x2﹣4x+1=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的两条边长分别为3和7,则它的周长为( )
A.10
B.13
C.17
D.13或17 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在△ABC中,AB=7,tanA=
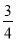 ,∠B=45°.点P从点A出发,沿AB方向以每秒1个单位长度的速度向终点B运动(不与点A、B重合),过点P作PQ⊥AB.交折线AC-CB于点Q,以PQ为边向右作正方形PQMN,设点P的运动时间为t(秒),正方形PQMN与△ABC重叠部分图形的面积为S(平方单位).
,∠B=45°.点P从点A出发,沿AB方向以每秒1个单位长度的速度向终点B运动(不与点A、B重合),过点P作PQ⊥AB.交折线AC-CB于点Q,以PQ为边向右作正方形PQMN,设点P的运动时间为t(秒),正方形PQMN与△ABC重叠部分图形的面积为S(平方单位).(1)直接写出正方形PQMN的边PQ的长(用含t的代数式表示).
(2)当点M落在边BC上时,求t的值.
(3)求S与t之间的函数关系式.
(4)如图②,点P运动的同时,点H从点B出发,沿B-A-B的方向做一次往返运动,在B-A上的速度为每秒2个单位长度,在A-B上的速度为每秒4个单位长度,当点H停止运动时,点P也随之停止,连结MH.设MH将正方形PQMN分成的两部分图形面积分别为S1、S2(平方单位)(0<S1<S2),直接写出当S2≥3S1时t的取值范围.
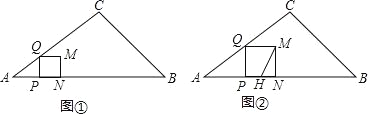
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的两边长是2和5,它的周长是( )
A.9
B.12
C.9或12
D.7
相关试题

