【题目】如图,等边三角形![]() 的边长为4厘米,长为1厘米的线段
的边长为4厘米,长为1厘米的线段![]() 在
在![]() 的边
的边![]() 上沿
上沿![]() 方向以1厘米/秒的速度向点
方向以1厘米/秒的速度向点![]() 运动(运动开始时,点
运动(运动开始时,点![]() 与点
与点![]() 重合,点
重合,点![]() 到达点
到达点![]() 时运动终止),过点
时运动终止),过点![]() 、
、![]() 分别作
分别作![]() 边的垂线,与
边的垂线,与![]() 的其他边交于
的其他边交于![]() 、
、![]() 两点.线段
两点.线段![]() 在运动的过程中,点
在运动的过程中,点![]() 、
、![]() 、
、![]() 、
、![]() 围成的图形的面积为
围成的图形的面积为![]() 平方厘米,运动的时间为
平方厘米,运动的时间为![]() 秒.则大致反映
秒.则大致反映![]() 与
与![]() 变化关系的图像是( )
变化关系的图像是( )

A.  .
. 
C. 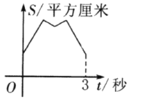 D.
D. 
参考答案:
【答案】A
【解析】
利用直角梯形的面积公式,由MN=1不变,可知四边形MNQP的面积随(PM+QN)的变化而变化,找到特殊点过点C作CG⊥AB,可分析得出四边形MNQP的面积变化情况.
解:过点C作CG⊥AB,
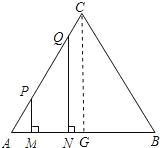
∵MN=1,四边形MNQP为直角梯形,
∴四边形MNQP的面积为S=![]() MN×(PM+QN),
MN×(PM+QN),
∴N点从A到G点四边形MNQP的面积为S=![]() MN×(PM+QN)中,PM,QN都在增大,所以面积也增大;
MN×(PM+QN)中,PM,QN都在增大,所以面积也增大;
当QN=CG时,QN开始减小,但PM仍然增大,且PM+QN不变,
∴四边形MNQP的面积不发生变化,
当PM<CG时,PM+QN开始减小,
∴四边形MNQP的面积减小,
∴符合要求的只有A.
故选:A.
-
科目: 来源: 题型:
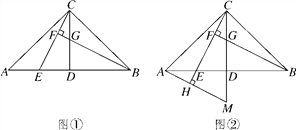
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠ACB=90°,D是AB的中点,点E是AB边上一点.
(1)BF⊥CE于点F,交CD于点G(如图①).求证:AE=CG;
(2)AH⊥CE,垂足为H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明.
-
科目: 来源: 题型:
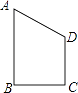
查看答案和解析>>【题目】四边形ABCD是直角梯形,AB∥CD,AB⊥BC,且BC=CD=2,AB=3,把梯形ABCD分别绕直线AB,CD旋转一周,所得几何体的表面积分别为S1 , S2 , 则|S1﹣S2|=(平方单位)
-
科目: 来源: 题型:
查看答案和解析>>【题目】射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,
 cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值(单位:秒)
cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值(单位:秒) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰梯形ABCD中,AB∥DC,线段AG,BG分别交CD于点E,F,DE=CF. 求证:△GAB是等腰三角形.

-
科目: 来源: 题型:
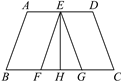
查看答案和解析>>【题目】如图所示,已知AD∥BC,AB∥EF,CD∥EG,且点E在直线AD上,点F,H,G在直线BC上,EH平分∠FEG,∠A=∠D=110°,线段EH的长是不是两条平行线AD,BC之间的距离?为什么?
-
科目: 来源: 题型:
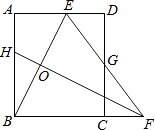
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,则BC的长是 .
相关试题

