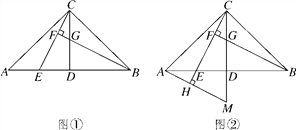
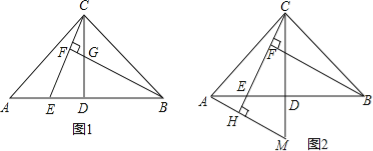
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,D是AB的中点,点E是AB边上一点.
(1)BF⊥CE于点F,交CD于点G(如图①).求证:AE=CG;
(2)AH⊥CE,垂足为H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明.
参考答案:
【答案】(1)证明见解析(2)BE=CM.证明见解析.
【解析】试题分析:(1)首先根据点D是AB中点,∠ACB=90°,可得出∠ACD=∠BCD=45°,判断出△AEC≌△CGB,即可得出AE=CG,
(2)根据垂直的定义得出∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,再根据AC=BC,∠ACM=∠CBE=45°,得出△BCE≌△CAM,进而证明出BE=CM.
(1)证明:∵点D是AB中点,AC=BC,
∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,
∴∠CAD=∠CBD=45°,
∴∠CAE=∠BCG,
又∵BF⊥CE,
∴∠CBG+∠BCF=90°,
又∵∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
在△AEC和△CGB中,
∴△AEC≌△CGB(ASA),
∴AE=CG,
(2)解:BE=CM.
证明:∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,
∴∠CMA=∠BEC,
又∵∠ACM=∠CBE=45°,
在△BCE和△CAM中, ,
,
∴△BCE≌△CAM(AAS),
∴BE=CM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图2是装有三个小轮的手拉车在“爬”楼梯时的侧面示意图,定长的轮架杆OA,OB,OC抽象为线段,有OA=OB=OC,且∠AOB=120°,折线NG﹣GH﹣HE﹣EF表示楼梯,GH,EF是水平线,NG,HE是铅垂线,半径相等的小轮子⊙A,⊙B与楼梯两边都相切,且AO∥GH.

(1)如图2①,若点H在线段OB时,则 的值是;
的值是;
(2)如果一级楼梯的高度HE=(8 +2)cm,点H到线段OB的距离d满足条件d≤3cm,那么小轮子半径r的取值范围是 .
+2)cm,点H到线段OB的距离d满足条件d≤3cm,那么小轮子半径r的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠C=90°,AB=2BC,现给出下列结论:①sinA=
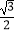 ;②cosB=
;②cosB=  ;③tanA=
;③tanA=  ;④tanB=
;④tanB=  ,其中正确的结论是(只需填上正确结论的序号)
,其中正确的结论是(只需填上正确结论的序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】杭州市某4所高中近两年的最低录取分数线如下表(单位:分),设4所高中2011年和2012年的平均最低录取分数线分别为
 ,
,  ,则
,则  =分 杭州市某4所高中最低录取分数线统计表
=分 杭州市某4所高中最低录取分数线统计表学校
2011年
2012年
杭州A中
438
442
杭州B中
435
442
杭州C中
435
439
杭州D中
435
439
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD是直角梯形,AB∥CD,AB⊥BC,且BC=CD=2,AB=3,把梯形ABCD分别绕直线AB,CD旋转一周,所得几何体的表面积分别为S1 , S2 , 则|S1﹣S2|=(平方单位)
-
科目: 来源: 题型:
查看答案和解析>>【题目】射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,
 cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值(单位:秒)
cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值(单位:秒) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形
 的边长为4厘米,长为1厘米的线段
的边长为4厘米,长为1厘米的线段 在
在 的边
的边 上沿
上沿 方向以1厘米/秒的速度向点
方向以1厘米/秒的速度向点 运动(运动开始时,点
运动(运动开始时,点 与点
与点 重合,点
重合,点 到达点
到达点 时运动终止),过点
时运动终止),过点 、
、 分别作
分别作 边的垂线,与
边的垂线,与 的其他边交于
的其他边交于 、
、 两点.线段
两点.线段 在运动的过程中,点
在运动的过程中,点 、
、 、
、 、
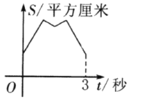
、 围成的图形的面积为
围成的图形的面积为 平方厘米,运动的时间为
平方厘米,运动的时间为 秒.则大致反映
秒.则大致反映 与
与 变化关系的图像是( )
变化关系的图像是( )
A.
 .
. 
C.
 D.
D. 
相关试题

