【题目】如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,则BC的长是 . 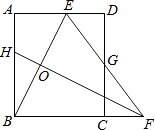
参考答案:
【答案】7
【解析】解:∵矩形ABCD中,G是CD的中点,AB=8, ∴CG=DG= ![]() ×8=4,
×8=4,
在△DEG和△CFG中,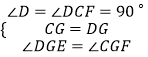 ,
,
∴△DEG≌△CFG(ASA),
∴DE=CF,EG=FG,
设DE=x,
则BF=BC+CF=AD+CF=4+x+x=4+2x,
在Rt△DEG中,EG= ![]() =
= ![]() ,
,
∴EF=2 ![]() ,
,
∵FH垂直平分BE,
∴BF=EF,
∴4+2x=2 ![]() ,
,
解得x=3,
∴AD=AE+DE=4+3=7,
∴BC=AD=7.
故答案为:7.
根据线段中点的定义可得CG=DG,然后利用“角边角”证明△DEG和△CFG全等,根据全等三角形对应边相等可得DE=CF,EG=FG,设DE=x,表示出BF,再利用勾股定理列式求EG,然后表示出EF,再根据线段垂直平分线上的点到两端点的距离相等可得BF=EF,然后列出方程求出x的值,从而求出AD,再根据矩形的对边相等可得BC=AD.
-
科目: 来源: 题型:
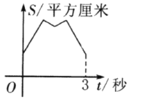
查看答案和解析>>【题目】如图,等边三角形
 的边长为4厘米,长为1厘米的线段
的边长为4厘米,长为1厘米的线段 在
在 的边
的边 上沿
上沿 方向以1厘米/秒的速度向点
方向以1厘米/秒的速度向点 运动(运动开始时,点
运动(运动开始时,点 与点
与点 重合,点
重合,点 到达点
到达点 时运动终止),过点
时运动终止),过点 、
、 分别作
分别作 边的垂线,与
边的垂线,与 的其他边交于
的其他边交于 、
、 两点.线段
两点.线段 在运动的过程中,点
在运动的过程中,点 、
、 、
、 、
、 围成的图形的面积为
围成的图形的面积为 平方厘米,运动的时间为
平方厘米,运动的时间为 秒.则大致反映
秒.则大致反映 与
与 变化关系的图像是( )
变化关系的图像是( )
A.
 .
. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰梯形ABCD中,AB∥DC,线段AG,BG分别交CD于点E,F,DE=CF. 求证:△GAB是等腰三角形.

-
科目: 来源: 题型:
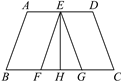
查看答案和解析>>【题目】如图所示,已知AD∥BC,AB∥EF,CD∥EG,且点E在直线AD上,点F,H,G在直线BC上,EH平分∠FEG,∠A=∠D=110°,线段EH的长是不是两条平行线AD,BC之间的距离?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y1=ax2+bx+c(a≠0)与x轴相交于点A,B(点A,B在原点O两侧),与y轴相交于点C,且点A,C在一次函数y2=
 x+n的图象上,线段AB长为16,线段OC长为8,当y1随着x的增大而减小时,求自变量x的取值范围.
x+n的图象上,线段AB长为16,线段OC长为8,当y1随着x的增大而减小时,求自变量x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某公司有三个住宅区可看作一点,A,B,C各区分别住有职工30人、15人、10人,且这三个住宅区在一条大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )

A. 点A B. 点B
C. A,B之间 D. B,C之间
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班有50位学生,每位学生都有一个序号,将50张编有学生序号(从1号到50号)的卡片(除序号不同外其它均相同)打乱顺序重新排列,从中任意抽取1张卡片.
(1)在序号中,是20的倍数的有:20,40,能整除20的有:1,2,4,5,10(为了不重复计数,20只计一次),求取到的卡片上序号是20的倍数或能整除20的概率;
(2)若规定:取到的卡片上序号是k(k是满足1≤k≤50的整数),则序号是k的倍数或能整除k(不重复计数)的学生能参加某项活动,这一规定是否公平?请说明理由;
(3)请你设计一个规定,能公平地选出10位学生参加某项活动,并说明你的规定是符合要求的.
相关试题

