【题目】综合题。
(1)计算:2﹣1+(2π﹣1)0﹣ ![]() ﹣sin45°﹣
﹣sin45°﹣ ![]() tan30°
tan30°
(2)解方程:x2+4x﹣1=0.
参考答案:
【答案】
(1)解:原式= ![]() +1﹣
+1﹣ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() ×
× ![]()
= ![]() +1﹣
+1﹣ ![]() ﹣1
﹣1
= ![]() ﹣
﹣ ![]()
(2)解:∵a=1,b=4,c=﹣1,
∴△=16﹣4×1×(﹣1)=20>0,
则x= ![]() =﹣2
=﹣2 ![]()
【解析】(1)根据实数的混合运算顺序和法则计算即可得;(2)公式法求解可得.
【考点精析】本题主要考查了零指数幂法则和整数指数幂的运算性质的相关知识点,需要掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【探究证明】
(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
如图1,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H.求证: =
=  ;
;
【结论应用】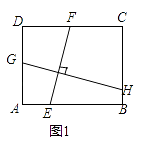
(2)如图2,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若 =
=  ,则
,则  的值为;
的值为;
【联系拓展】
(3)如图3,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求 的值.
的值.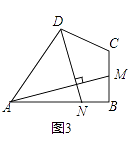
-
科目: 来源: 题型:
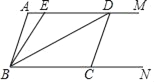
查看答案和解析>>【题目】如图,两条射线AM∥BN,线段CD的两个端点C、D分别在射线BN、AM上,且∠A=∠BCD=108°.E是线段AD上一点(不与点A、D重合),且BD平分∠EBC.
(1)求∠ABC的度数.
(2)请在图中找出与∠ABC相等的角,并说明理由.
(3)若平行移动CD,且AD>CD,则∠ADB与∠AEB的度数之比是否随着CD位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,抛物线y=﹣
 x2+bx+c与x轴交与点A(﹣3,0),点B(9,0),与y轴交与点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
x2+bx+c与x轴交与点A(﹣3,0),点B(9,0),与y轴交与点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
(1)求抛物线的解析式;
(2)过点P作BD的平行线,交AB于点Q,连接DQ,设AQ=m,△PDQ的面积为S,求S关于m的函数解析式,以及S的最大值;
(3)如图2,抛物线对称轴与x轴交与点G,E为OG的中点,F为点C关于DG对称的对称点,过点P分别作直线EF、DG的垂线,垂足为M、N,连接MN,当△PMN为等腰三角形时,求此时EM的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个不透明的口袋,甲口袋中装有3个分别标有数字1、2、3的小球,乙口袋中装有分别标有数字4、5的小球,它们的形状、大小完全相同,现随机从甲口袋中摸出一个小球记下数字,再从乙口袋中摸出一个小球记下数字.请用列表或树状图的方法(只选其中一种)求出两个数字之和能被3整除的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+2与双曲线相交于点A(m,3),与x轴交于点C.
x+2与双曲线相交于点A(m,3),与x轴交于点C. 
(1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D、E,AD与BE相交于点F.

(1)求证:△ACD∽△BFD;
(2)若∠ABD=45°,AC=3时,求BF的长.
相关试题

