【题目】如图,直线y= ![]() x+2与双曲线相交于点A(m,3),与x轴交于点C.
x+2与双曲线相交于点A(m,3),与x轴交于点C. 
(1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
参考答案:
【答案】
(1)解:把A(m,3)代入直线解析式得:3= ![]() m+2,即m=2,
m+2,即m=2,
∴A(2,3),
把A坐标代入y= ![]() ,得k=6,
,得k=6,
则双曲线解析式为y= ![]()
(2)解:对于直线y= ![]() x+2,令y=0,得到x=﹣4,即C(﹣4,0),
x+2,令y=0,得到x=﹣4,即C(﹣4,0),
设P(x,0),可得PC=|x+4|,
∵△ACP面积为3,
∴ ![]() |x+4|3=3,即|x+4|=2,
|x+4|3=3,即|x+4|=2,
解得:x=﹣2或x=﹣6,
则P坐标为(﹣2,0)或(﹣6,0)
【解析】(1)把A坐标代入直线解析式求出m的值,确定出A坐标,即可确定出双曲线解析式;(2)设P(x,0),表示出PC的长,高为A纵坐标,根据三角形ACP面积求出x的值,确定出P坐标即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,抛物线y=﹣
 x2+bx+c与x轴交与点A(﹣3,0),点B(9,0),与y轴交与点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
x2+bx+c与x轴交与点A(﹣3,0),点B(9,0),与y轴交与点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
(1)求抛物线的解析式;
(2)过点P作BD的平行线,交AB于点Q,连接DQ,设AQ=m,△PDQ的面积为S,求S关于m的函数解析式,以及S的最大值;
(3)如图2,抛物线对称轴与x轴交与点G,E为OG的中点,F为点C关于DG对称的对称点,过点P分别作直线EF、DG的垂线,垂足为M、N,连接MN,当△PMN为等腰三角形时,求此时EM的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)计算:2﹣1+(2π﹣1)0﹣ ﹣sin45°﹣
﹣sin45°﹣ 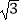 tan30°
tan30°
(2)解方程:x2+4x﹣1=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个不透明的口袋,甲口袋中装有3个分别标有数字1、2、3的小球,乙口袋中装有分别标有数字4、5的小球,它们的形状、大小完全相同,现随机从甲口袋中摸出一个小球记下数字,再从乙口袋中摸出一个小球记下数字.请用列表或树状图的方法(只选其中一种)求出两个数字之和能被3整除的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D、E,AD与BE相交于点F.

(1)求证:△ACD∽△BFD;
(2)若∠ABD=45°,AC=3时,求BF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=
 ∠CAB.
∠CAB. 
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF= ,求BC和BF的长.
,求BC和BF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如表:
x
…
﹣2
﹣1
0
1
2
…
y
…
0
4
6
6
4
…
从上表可知,有下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴是x=1;
③抛物线与x轴有两个交点,它们之间的距离是 ;
;
④在对称轴左侧y随x增大而增大.
其中正确的说法是( )
A.①②③
B.②③④
C.②③
D.①④
相关试题

