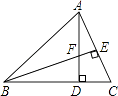
【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D、E,AD与BE相交于点F. 
(1)求证:△ACD∽△BFD;
(2)若∠ABD=45°,AC=3时,求BF的长.
参考答案:
【答案】
(1)证明:如图,∵AD⊥BC,BE⊥AC
∴∠BDF=∠ADC=∠BEC=90°
∴∠C+∠DBF=90°,∠C+∠DAC=90°
∴∠DBF=∠DAC
∴△ACD∽△BFD
(2)解:如图,∵∠ABD=45°,∠ADB=90°,
∴AD=BD,
∴ ![]() =1,
=1,
∵△ACD∽△BFD,AC=3,
∴ ![]() =1,
=1,
∴BF=AC=3.
【解析】(1)只要证明∠DBF=∠DAC,即可判断.(2)利用相似三角形的性质即可解决问题.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)计算:2﹣1+(2π﹣1)0﹣ ﹣sin45°﹣
﹣sin45°﹣ 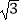 tan30°
tan30°
(2)解方程:x2+4x﹣1=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个不透明的口袋,甲口袋中装有3个分别标有数字1、2、3的小球,乙口袋中装有分别标有数字4、5的小球,它们的形状、大小完全相同,现随机从甲口袋中摸出一个小球记下数字,再从乙口袋中摸出一个小球记下数字.请用列表或树状图的方法(只选其中一种)求出两个数字之和能被3整除的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+2与双曲线相交于点A(m,3),与x轴交于点C.
x+2与双曲线相交于点A(m,3),与x轴交于点C. 
(1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=
 ∠CAB.
∠CAB. 
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF= ,求BC和BF的长.
,求BC和BF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如表:
x
…
﹣2
﹣1
0
1
2
…
y
…
0
4
6
6
4
…
从上表可知,有下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴是x=1;
③抛物线与x轴有两个交点,它们之间的距离是 ;
;
④在对称轴左侧y随x增大而增大.
其中正确的说法是( )
A.①②③
B.②③④
C.②③
D.①④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与双曲线
与双曲线  交于点A.将直线
交于点A.将直线  向右平移6个单位后,与双曲线
向右平移6个单位后,与双曲线  交于点B,与x轴交于点C,若
交于点B,与x轴交于点C,若  ,则k的值为( )
,则k的值为( ) 
A.12
B.14
C.18
D.24
相关试题

