【题目】下列说法不正确的是( )
A.因为M是线段AB的中点,所以AM=MB=![]() AB
AB
B.在线段AM延长线上取一点B,如果AB=2AM,那么点M是线段AB的中点
C.因为A,M,B在同一直线上,且AM=MB,所以M是线段AB的中点
D.因为AM=MB,所以点M是AB的中点
参考答案:
【答案】D
【解析】
根据线段中点的定义:线段上一点,到线段两端点距离相等的点,可进行判断解答.
A. 因为M是线段AB的中点,所以AM=MB=![]() AB,正确;
AB,正确;
B. 在线段AM延长线上取一点B,如果AB=2AM,那么点M是线段AB的中点,正确;
C. 因为A,M,B在同一直线上,且AM=MB,所以M是线段AB的中点,正确;
D. 当AM=MB,M在线段AB上,点M才是AB的中点,故D错误;
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO︰S△BCO︰S△CAO等于( )

A. 1︰1︰1
B. 1︰2︰3
C. 2︰3︰4
D. 3︰4︰5
-
科目: 来源: 题型:
查看答案和解析>>【题目】感知:如图①,△ABC是等腰直角三角形,∠ACB=90°,正方形CDEF的顶点D、F分别在边AC、BC上,易证:AD=BF(不需要证明);
探究:将图①的正方形CDEF绕点C顺时针旋转α(0°<α<90°),连接AD、BF,其他条件不变,如图②,求证:AD=BF;
应用:若α=45°,CD=
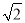 ,BE=1,如图③,则BF= .
,BE=1,如图③,则BF= .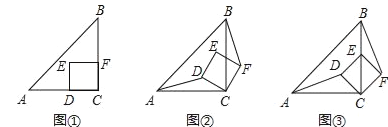
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E、F分别为AB、BC的中点,连接CE、DF,将△CBE沿CE对折,得到△CGE,延长EG交CD的延长线于点H。

(1)求证:CE⊥DF;
(2)求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使三角形AMN周长最小时,则∠AMN+∠ANM的度数为( )

A. 80° B. 90° C. 100° D. 130°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在数轴上点
 表示数
表示数 ,点
,点 表示数
表示数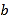 ,点
,点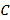 表示数
表示数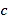 ,
,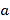 是多项式
是多项式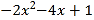 的一次项系数,
的一次项系数,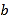 是绝对值最小的整数,单项式
是绝对值最小的整数,单项式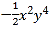 的次数为
的次数为 .
.
(1)
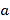 = ,
= ,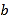 = ,
= ,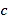 = ;
= ;(2)若将数轴在点
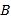 处折叠,则点
处折叠,则点 与点
与点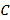 重合( 填“能”或“不能”);
重合( 填“能”或“不能”);(3)点
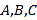 开始在数轴上运动,若点
开始在数轴上运动,若点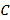 以每秒1个单位长度的速度向右运动,同时,点
以每秒1个单位长度的速度向右运动,同时,点 和点
和点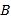 分别以每秒3个单位长度和2个单位长度的速度向左运动,
分别以每秒3个单位长度和2个单位长度的速度向左运动,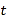 秒钟过后,若点
秒钟过后,若点 与点B之间的距离表示为
与点B之间的距离表示为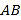 ,点
,点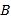 与点
与点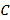 之间的距离表示为
之间的距离表示为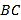 ,则
,则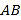 = ,
= , 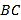 = (用含
= (用含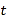 的代数式表示);
的代数式表示);(4)请问:AB+BC的值是否随着时间
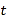 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一刻度尺放在数轴上.

①若刻度尺上 0cm 和 4cm 对应数轴上的点表示的数分别为 1 和 5,则 1cm 对应数轴上的点表示的数是 2;
②若刻度尺上 0cm 和 4cm 对应数轴上的点表示的数分别为 1 和 9,则 1cm 对应数轴上的点表示的数是 3;
③若刻度尺上 0cm 和 4cm 对应数轴上的点表示的数分别为-2 和 2,则 1cm 对应数轴上的点表示的数是-1;
④若刻度尺上 0cm 和 4 cm 对应数轴上的点表示的数分别为-1 和 1,则 1cm 对应数轴上的点表示的数是-0.5. 上述结论中,所有正确结论的序号是 ( )
A.①②B.②④C.①②③D.①②③④
相关试题

