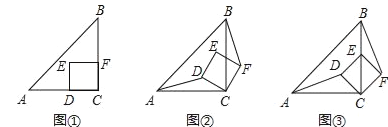
【题目】感知:如图①,△ABC是等腰直角三角形,∠ACB=90°,正方形CDEF的顶点D、F分别在边AC、BC上,易证:AD=BF(不需要证明);
探究:将图①的正方形CDEF绕点C顺时针旋转α(0°<α<90°),连接AD、BF,其他条件不变,如图②,求证:AD=BF;
应用:若α=45°,CD=![]() ,BE=1,如图③,则BF= .
,BE=1,如图③,则BF= .
参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】试题分析: 探究:证明△ADC≌△BFC,可得结论;
应用:过D作DG⊥AC于G,先根据勾股定理得:EC=2,得正方形边长为3,则AC=3,根据α=45°,得△DCG是等腰直角三角形,求出CG的长,则得AG的长,再次利用勾股定理求AD的长,即BF的长.
试题解析:
证明:探究:如图②,
四边形CDEF为正方形,
∴CD=CF,
由旋转得:∠ACD=∠BCF,
△ABC是等腰直角三角形,∠ACB=90°,
∴AC=BC,
△ADC≌△BFC,
∴AD=BF;
应用:如图③,
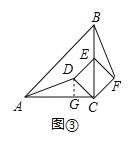
∵四边形CDEF为正方形,
∠EDC=90° ED=DC,
![]()
![]() ,
,
∴BC=BE+EC=1+2=3,
∴AC=BC=3,
过D作DG⊥AC于G,
∵a=45°,
即∠ACD=45,
∴△DCG是等腰直角三角形,
∴DG=CG=1,
∴AG=BC-CG=3-1=2,
由勾股定理得: ![]() ,
,
同理得:△ADC≌△BFC,
![]()
点睛: 本题是四边形和图形旋转的综合题,考查了正方形、等腰直角三角形、全等三角形的性质,熟知正方形的各边相等,各角都是90°,等腰直角三角形的两直角边相等,且锐角为45°;明确旋转角相等,同时利用三角形全等和勾股定理求边和角的度数,使问题得以解决.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下:

根据上述信息完成下列问题:
(1)求这次抽取的样本的容量;
(2)请在图②中把条形统计图补充完整;
(3)已知该校这次活动共收到参赛作品750份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,AB=4,AD是BC边上的中线,将△ABD绕点A旋转,使AB与AC重合,连接DE,则线段DE的长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆有50个房间供游客居住,当每个房间每天的定价为180元时,房间会全部住满;当每个房间每天的定价每增加10元时,就会有一个房间空闲.如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用.
(1)若每个房间定价增加40元,则这个宾馆这一天的利润为多少元?
(2)若宾馆某一天获利10640元,则房价定为多少元?
(3)房价定为多少时,宾馆的利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体水槽,使它的底面积为800平方厘米.求截去正方形的边长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解不等式
 ;
;(2)求不等式
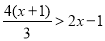 的正整数解;
的正整数解;(3)解不等式组
 ;
;(4)解不等式组
 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
相关试题

