【题目】如图:在数轴上点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,
,![]() 是多项式
是多项式![]() 的一次项系数,
的一次项系数,![]() 是绝对值最小的整数,单项式
是绝对值最小的整数,单项式![]() 的次数为
的次数为![]() .
.
![]()
(1)![]() = ,
= ,![]() = ,
= ,![]() = ;
= ;
(2)若将数轴在点![]() 处折叠,则点
处折叠,则点![]() 与点
与点![]() 重合( 填“能”或“不能”);
重合( 填“能”或“不能”);
(3)点![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒1个单位长度的速度向右运动,同时,点
以每秒1个单位长度的速度向右运动,同时,点![]() 和点
和点![]() 分别以每秒3个单位长度和2个单位长度的速度向左运动,
分别以每秒3个单位长度和2个单位长度的速度向左运动,![]() 秒钟过后,若点
秒钟过后,若点![]() 与点B之间的距离表示为
与点B之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,则
,则![]() = ,
= , ![]() = (用含
= (用含![]() 的代数式表示);
的代数式表示);
(4)请问:AB+BC的值是否随着时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
参考答案:
【答案】(1)a= -4 ,b= 0,c=6;(2)不能 ;(3)B=t+4,BC= 3t + 6;(4)AB+BC的值是随着时间t的变化而改变.
【解析】
(1)根据多项式与单项式的概念即可求出答案;
(2)根据a、b、c的值确定A、C是否关于点B对称即可;
(3)根据A、B、C三点的运动速度和运动方向可得;
(4)将(3)中的AB与BC的表达式代入即可判断.
(1)∵多项式![]() 的一次项系数为-4,绝对值最小的整数是0,单项式
的一次项系数为-4,绝对值最小的整数是0,单项式![]() 的次数为6,
的次数为6,
∴a=-4,b=0,c=6;
(2)不能重合,由-4和6的中点为1,故将数轴在点B出折叠,点A和点C不能重合;
(3)由于点![]() 和点
和点![]() 分别以每秒3个单位长度和2个单位长度的速度向左运动,
分别以每秒3个单位长度和2个单位长度的速度向左运动,
∴![]() 秒钟过后,AB=3t+4-2t=t+4;
秒钟过后,AB=3t+4-2t=t+4;
由于点![]() 以每秒1个单位长度的速度向右运动,
以每秒1个单位长度的速度向右运动,
∴![]() 秒钟过后,BC=2t+6+t=3t+6;
秒钟过后,BC=2t+6+t=3t+6;
(4)AB+BC=(t+4)+(3t+6)=4t+10,
所以,AB+BC的值是随着时间t的变化而改变.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E、F分别为AB、BC的中点,连接CE、DF,将△CBE沿CE对折,得到△CGE,延长EG交CD的延长线于点H。

(1)求证:CE⊥DF;
(2)求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是( )
A.因为M是线段AB的中点,所以AM=MB=
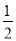 AB
ABB.在线段AM延长线上取一点B,如果AB=2AM,那么点M是线段AB的中点
C.因为A,M,B在同一直线上,且AM=MB,所以M是线段AB的中点
D.因为AM=MB,所以点M是AB的中点
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使三角形AMN周长最小时,则∠AMN+∠ANM的度数为( )

A. 80° B. 90° C. 100° D. 130°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一刻度尺放在数轴上.

①若刻度尺上 0cm 和 4cm 对应数轴上的点表示的数分别为 1 和 5,则 1cm 对应数轴上的点表示的数是 2;
②若刻度尺上 0cm 和 4cm 对应数轴上的点表示的数分别为 1 和 9,则 1cm 对应数轴上的点表示的数是 3;
③若刻度尺上 0cm 和 4cm 对应数轴上的点表示的数分别为-2 和 2,则 1cm 对应数轴上的点表示的数是-1;
④若刻度尺上 0cm 和 4 cm 对应数轴上的点表示的数分别为-1 和 1,则 1cm 对应数轴上的点表示的数是-0.5. 上述结论中,所有正确结论的序号是 ( )
A.①②B.②④C.①②③D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在数轴上表示下列各数,并用“<”号把它们连接.
3, -1, 0, -2.5, 1.5, 2

(2)快递员要从物流中心出发送货,已知甲住户在物流中心的东边 2km 处,乙住户在甲住户的西边 3km 处,丙住户在物流中心的西边 1.5km 处,请建立数轴表示物流中心、甲住户、乙住户、丙住户的位置关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,…,依次规律,第( )个图形有76个小圆.

A. 8 B. 9 C. 10 D. 11
相关试题

