【题目】四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使三角形AMN周长最小时,则∠AMN+∠ANM的度数为( )

A. 80° B. 90° C. 100° D. 130°
参考答案:
【答案】C
【解析】作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.
解:作DA延长线A A″,
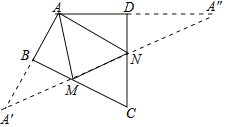
∵∠DAB=130°,
∴∠HAA′=50°,
∴∠AA′M+∠A″=∠HAA′=50°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×50°=100°,
故选C.
“点睛”本题考查的是轴对称-最短路线问题,涉及到平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出M、N的位置是解题关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列方程,属于一元一次方程的是( )
A. 2x-(1-x) B. x-xy=0 C. 2y2+y-1=0 D. x=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次数学竞赛初试有试题25道,阅卷规定:每答对一题得4分,每答错(包括未答)一题得(﹣1)分,得分不低于60分则可以参加复试.那么,若要参加复试,初试的答对题数至少为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)2x2+4x﹣3=0(配方法解)
(2)5x2﹣8x+2=0(公式法解)
(3)3(x﹣5)2=2(5﹣x)
(4)(3x+2)(x+3)=x+14.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 (2016湖北随州第12题)已知等腰三角形的一边长为9,另一边长为方程x2﹣8x+15=0的根,则该等腰三角形的周长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个数的立方根是1,则这个数是
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,求∠AEB的度数.
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请求∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
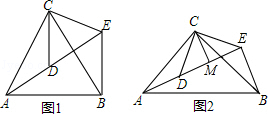
相关试题

